
1、用向量解的同学可能会感觉稍稍舒服一点。简答题里的第十八题这道题来看,还有刚才我提到的第七小题,这两道题我的感觉,因为我没有继续做得太多,感觉用向量法的同学会稍稍简单一些。这也还是体现了新课程对立体几何教学的一个渗透。这两道题还是大纲卷,但在课标卷或者新课标卷中,对解决向量解决立体几何是理科同学必须要学的内容,所以我们要特别关注新课标对我们高三同学对大纲教学的理解和渗透。
21.(本小题满分14分)
已知二次函数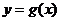 的导函数的图像与直线
的导函数的图像与直线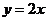 平行,且
平行,且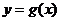 在
在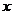 =-1处取得最小值m-1(m
=-1处取得最小值m-1(m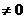 ).设函数
).设函数
(1)若曲线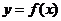 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为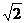 ,求m的值
,求m的值
(2) 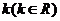 如何取值时,函数
如何取值时,函数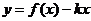 存在零点,并求出零点.
存在零点,并求出零点.
[解析](1)设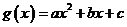 ,则
,则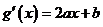 ;
;
又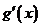 的图像与直线
的图像与直线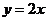 平行
平行
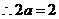
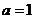
又 在
在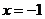 取极小值,
取极小值,
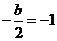 ,
, 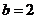
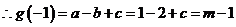 ,
, 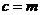 ;
;
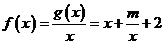 ,
设
,
设
则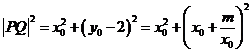
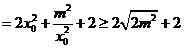
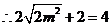
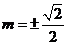 ;
; 

(2)由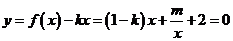 ,
,
得 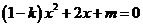

当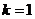 时,方程
时,方程 有一解
有一解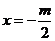 ,函数
,函数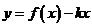 有一零点
有一零点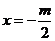 ;
;
当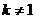 时,方程
时,方程 有二解
有二解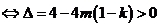 ,若
,若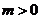 ,
,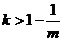 ,
,
函数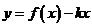 有两个零点
有两个零点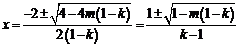 ;若
;若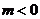 ,
,
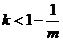 ,函数
,函数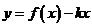 有两个零点
有两个零点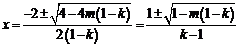 ;
;
当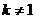 时,方程
时,方程 有一解
有一解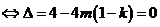 ,
, 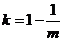 , 函数
, 函数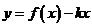 有一零点
有一零点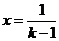


20.(本小题满分14分)
已知点(1, )是函数
)是函数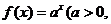 且
且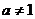 )的图象上一点,等比数列
)的图象上一点,等比数列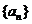 的前n项和为
的前n项和为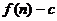 ,数列
,数列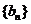
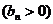 的首项为c,且前n项和
的首项为c,且前n项和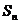 满足
满足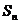 -
-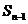 =
=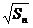 +
+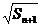 (n
(n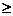 2).
2).
(1)求数列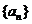 和
和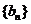 的通项公式;
的通项公式;
(2)若数列{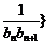 前n项和为
前n项和为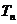 ,问
,问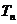 >
>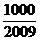 的最小正整数n是多少?
的最小正整数n是多少?
[解析](1)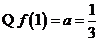 ,
,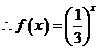


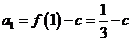 ,
,
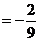 ,
,
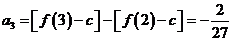 .
.
又数列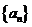 成等比数列,
成等比数列, ,所以
,所以 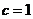 ;
;
又公比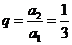 ,所以
,所以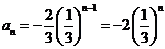
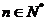 ;
;
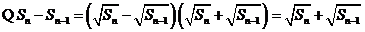
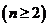
又 ,
,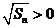 ,
, 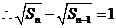 ;
;
数列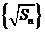 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,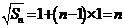 ,
, 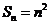
当 ,
, 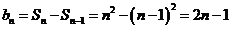 ;
;
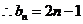 (
(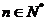 );
);
(2)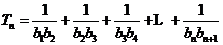
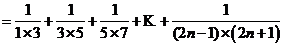
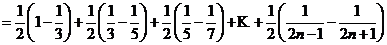
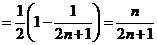 ;
; 

由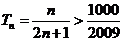 得
得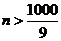 ,满足
,满足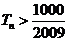 的最小正整数为112.
的最小正整数为112.
19.(本小题满分14分)
已知椭圆G的中心在坐标原点,长轴在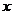 轴上,离心率为
轴上,离心率为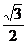 ,两个焦点分别为
,两个焦点分别为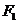 和
和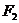 ,椭圆G上一点到
,椭圆G上一点到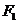 和
和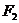 的距离之和为12.圆
的距离之和为12.圆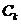 :
: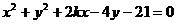
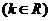 的圆心为点
的圆心为点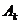 .
.
(1)求椭圆G的方程
(2)求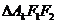 的面积
的面积
(3)问是否存在圆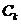 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
[解析](1)设椭圆G的方程为: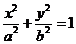 (
(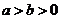 )半焦距为c;
)半焦距为c;
则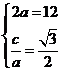 , 解得
, 解得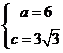 ,
, 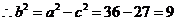
所求椭圆G的方程为: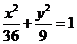 .
.


(2 )点 的坐标为
的坐标为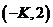
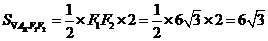
(3)若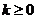 ,由
,由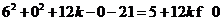 可知点(6,0)在圆
可知点(6,0)在圆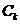 外,
外,
若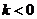 ,由
,由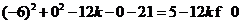 可知点(-6,0)在圆
可知点(-6,0)在圆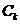 外;
外;
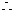 不论K为何值圆
不论K为何值圆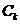 都不能包围椭圆G.
都不能包围椭圆G.
18.(本小题满分13分)
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
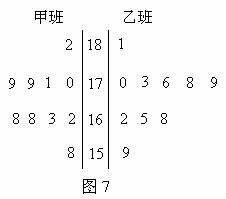
[解析](1)由茎叶图可知:甲班身高集中于 之间,而乙班身高集中于
之间,而乙班身高集中于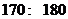 之间。因此乙班平均身高高于甲班;
之间。因此乙班平均身高高于甲班;
(2) 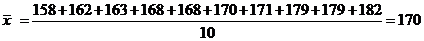
甲班的样本方差为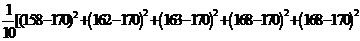
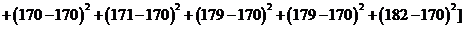 =57
=57
(3)设身高为176cm的同学被抽中的事件为A;
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10个基本事件,而事件A含有4个基本事件;
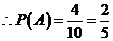 ;
;
17.(本小题满分13分)
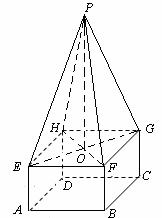
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD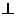 平面PEG
平面PEG
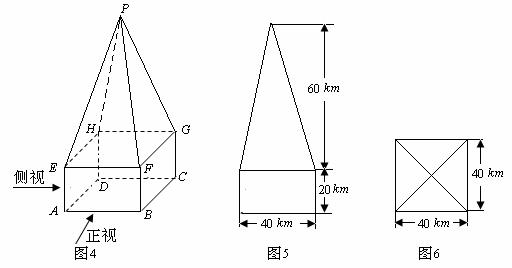
[解析](1)侧视图同正视图,如下图所示.
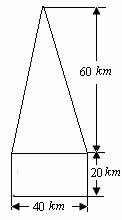
(2)该安全标识墩的体积为: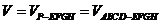
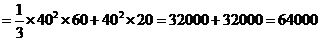
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知,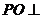 平面EFGH ,
平面EFGH , 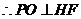
又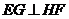
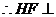 平面PEG
平面PEG
又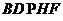
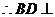 平面PEG;
平面PEG; 

16.(本小题满分12分)
已知向量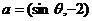 与
与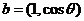 互相垂直,其中
互相垂直,其中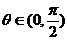
(1)求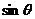 和
和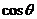 的值
的值
(2)若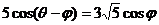 ,
,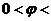
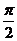 ,求
,求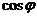 的值
的值
[解析](1)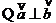 ,
,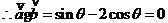 ,即
,即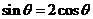
又∵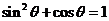 , ∴
, ∴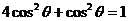 ,即
,即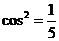 ,∴
,∴
又 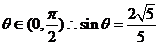 ,
,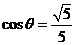
(2) ∵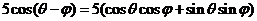
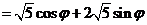
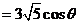
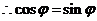 ,
,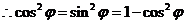 ,即
,即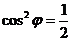
又 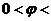
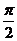 , ∴
, ∴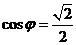


(二)选做题(14、15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)若直线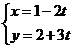 (t为参数)与直线
(t为参数)与直线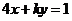 垂直,则常数
垂直,则常数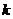 = .
= .
[答案]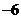
[解析]将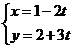 化为普通方程为
化为普通方程为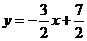 ,斜率
,斜率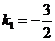 ,
,
当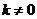 时,直线
时,直线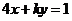 的斜率
的斜率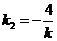 ,由
,由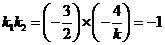 得
得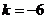 ;
;
当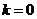 时,直线
时,直线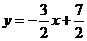 与直线
与直线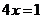 不垂直.
不垂直.
综上可知,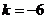 .
.
15.(几何证明选讲选做题)如图3,点A、B、C是圆O上的点,且AB=4,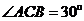 ,则圆O的面积等于 .
,则圆O的面积等于 . 

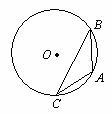
图3
[答案]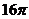
[解析]连结AO,OB,因为 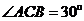 ,所以
,所以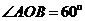 ,
,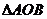 为等边三角形,故圆O的半径
为等边三角形,故圆O的半径 ,圆O的面积
,圆O的面积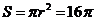 .
.
(一)必做题(11-13题)
11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
|
队员i |
1 |
2 |
3 |
4 |
5 |
6 |
|
三分球个数 |
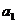 |
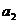 |
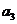 |
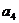 |
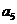 |
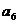 |
图1是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填 ,输出的s=
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)



图1
[答案]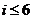 ,
,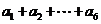
[解析]顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,所图中判断框应填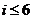 ,输出的s=
,输出的s= .
.
12.某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是 。若用分层抽样方法,则40岁以下年龄段应抽取 人.
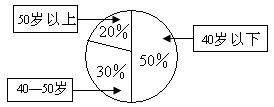
图 2
[答案]37, 20
[解析]由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为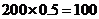 ,则应抽取的人数为
,则应抽取的人数为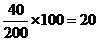 人.
人.
13.以点(2,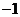 )为圆心且与直线
)为圆心且与直线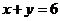 相切的圆的方程是
.
相切的圆的方程是
.
[答案]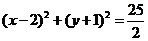
[解析]将直线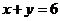 化为
化为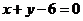 ,圆的半径
,圆的半径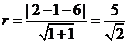 ,所以圆的方程为
,所以圆的方程为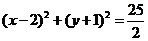


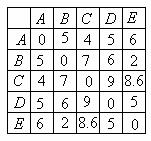
10.广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表.若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短路线距离是
A.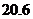 B.21 C.22 D.23
B.21 C.22 D.23


[答案]B
[解析]由题意知,所有可能路线有6种:
①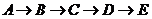 ,②
,②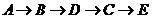 ,③
,③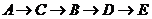 ,④
,④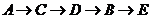 ,⑤
,⑤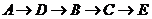 ,⑥
,⑥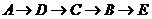 ,
,
其中, 路线③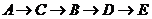 的距离最短, 最短路线距离等于
的距离最短, 最短路线距离等于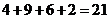 ,
,
故选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com