
2.(2005湖北)双曲线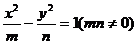 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线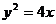 的焦点重合,则mn的值为 ( )
的焦点重合,则mn的值为 ( )
A.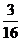 B.
B.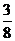 C.
C.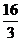 D.
D.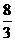
1.(2004湖北)已知椭圆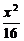 +
+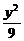 =1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 ( )
=1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 ( )
A.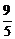 B.3
C.
B.3
C.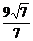 D.
D.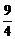
5.注意用好以下数学思想、方法:
①数形结合思想;②方程与函数思想;③化归转化思想;④分类讨论思想;⑤对称思想;⑥主元与参数思想.此外,整体思想、正难则反思想、构造思想等也是解析几何解题中不可缺少的思想方法.在复习中必须给予足够的重视,真正发挥其联系知识、简化计算、提高能力中的作用.
同步练习 8.5 圆锥曲线综合应用
[选择题]
4.四点重视:①重视定义在解题中的作用;②重视平面几何知识在解题中的简化功能;③重视根与系数关系在解题中的作用;④重视曲线的几何特征与方程的代数特征的统一.
3. 解决圆锥曲线应用问题时,要善于抓住问题的实质,通过建立数学模型,实现应用性问题向数学问题的顺利转化;要注意认真分析数量间的关系,紧扣圆锥曲线概念,充分利用曲线的几何性质,确定正确的问题解决途径,灵活运用解析几何的常用数学方法,求得最终完整的解答.
2.对于求曲线方程中参数范围或最值问题,应根据题设条件及曲线的几何性质构造参数满足的不等式,通过解不等式求得参数的范围;或建立关于参数的目标函数,转化为函数的值域来解,还有Δ法,几何法,向量法等.
1.解决圆锥曲线的综合问题应根据曲线的几何特征,熟练运用圆锥曲线的知识将曲线的几何特征转化为数量关系,再结合代数等知识来解。
[例1](2006福建) 已知椭圆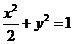 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线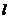 相切的圆的方程;
相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与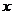 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
解:(I)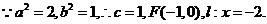
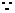 圆过点O、F,
圆过点O、F,
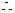 圆心M在直线
圆心M在直线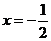 上。
上。
设 则圆半径
则圆半径
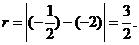
由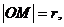 得
得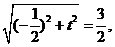
解得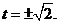
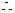 所求圆的方程为
所求圆的方程为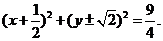
(II)设直线AB的方程为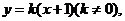
代入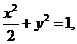 整理得
整理得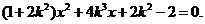
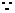 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,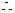 方程有两个不等实根。
方程有两个不等实根。
记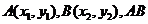 中点
中点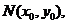
则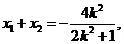
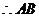 的垂直平分线NG的方程为
的垂直平分线NG的方程为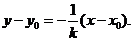
令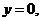 得
得

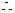 点G横坐标的取值范围为
点G横坐标的取值范围为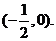
[例2](2006天津)如图,以椭圆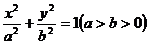 的中心
的中心 为圆心,分别以
为圆心,分别以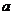 和
和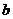 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点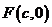
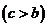 作垂直于
作垂直于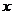 轴的直线交大圆于第一象限内的点
轴的直线交大圆于第一象限内的点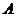 .连结
.连结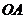 交小圆于点
交小圆于点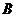 .设直线
.设直线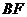 是小圆的切线.
是小圆的切线.
 (1)证明
(1)证明 ,并求直线
,并求直线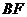 与
与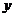 轴的交
轴的交
点 的坐标;
的坐标;
(2)设直线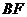 交椭圆于
交椭圆于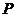 、
、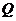 两点,证明
两点,证明
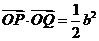 .
.
(Ⅰ)证明:由题设条件知,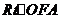 ∽
∽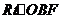 故
故
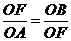 ,即
,即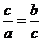
因此,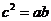 ①
①
解:在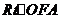 中
中
 .
.
于是,直线OA的斜率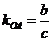 .设直线BF的斜率为
.设直线BF的斜率为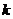 ,则
,则
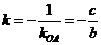 .
.
这时,直线BF与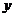 轴的交点为
轴的交点为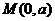
(Ⅱ)证明:由(Ⅰ),得直线BF得方程为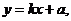 且
且
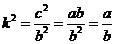 ②
②
由已知,设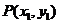 、
、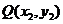 ,则它们的坐标满足方程组
,则它们的坐标满足方程组
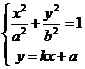 ③
③
由方程组③消去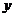 ,并整理得
,并整理得
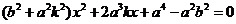 ④
④
由式①、②和④,
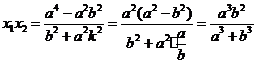
由方程组③消去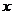 ,并整理得
,并整理得
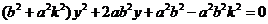 ⑤
⑤
由式②和⑤,
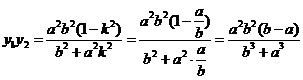
综上,得到
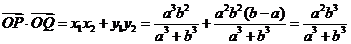
注意到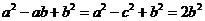 ,得
,得
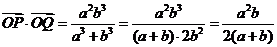

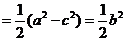
[例3]A、B、C是我方三个炮兵阵地,A在B正东6 km,C在B正北偏西30°,相距4 km,P为敌炮阵地,某时刻A处发现敌炮阵地的某种信号,由于B、C两地比A距P地远,因此4 s后,B、C才同时发现这一信号,此信号的传播速度为1 km/s,A若炮击P地,求炮击的方位角.
解:如下图,以直线BA为x轴,线段BA的中垂线为y轴建立坐标系,则
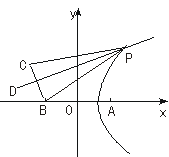 B(-3,0)、A(3,0)、C(-5,2
B(-3,0)、A(3,0)、C(-5,2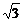 ).
).
因为|PB|=|PC|,所以点P在线段BC的垂直平分线上.
因为kBC=-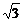 ,BC中点D(-4,
,BC中点D(-4,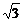 ),
),
所以直线PD的方程为y-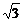 =
=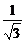 (x+4) ①
(x+4) ①
又|PB|-|PA|=4,故P在以A、B为焦点的双曲线右支上.
设P(x,y),则双曲线方程为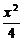 -
-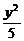 =1(x≥0) ②
=1(x≥0) ②
联立①②,得x=8,y=5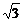 ,
,
所以P(8,5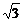 ).因此kPA=
).因此kPA=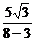 =
=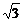 .
.
故炮击的方位角为北偏东30°.
[例4] (2006春上海) 学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为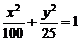 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以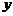 轴为对称轴、
轴为对称轴、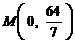 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为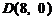 . 观测点
. 观测点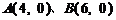 同时跟踪航天器.
同时跟踪航天器.
 (1)求航天器变轨后的运行轨迹所在的曲线方程;
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在 轴上方时,观测点
轴上方时,观测点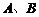 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
解(1)设曲线方程为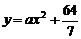 , 由题意可知,
, 由题意可知,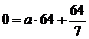 .
. 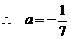 .
.
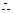 曲线方程为
曲线方程为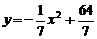
(2)设变轨点为 ,根据题意可知
,根据题意可知
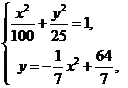 得
得
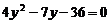 ,
,
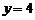 或
或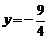 (不合题意,舍去).
(不合题意,舍去).
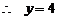 . 得
. 得 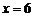 或
或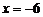 (不合题意,舍去).
(不合题意,舍去).
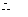
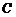 点的坐标为
点的坐标为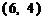 ,
, 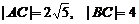 .
.
答:当观测点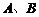 测得
测得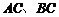 距离分别为
距离分别为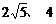 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.
[研讨.欣赏](2006重庆)已知一列椭圆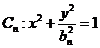 ,
,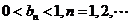 。若椭圆
。若椭圆 上有一点
上有一点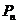 ,使
,使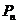 到右准线
到右准线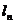 的距离
的距离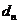 是
是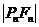 与
与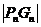 的等差中项,其中
的等差中项,其中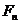 、
、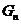 分别是
分别是 的左、右焦点。
的左、右焦点。
(Ⅰ)试证: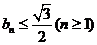 ;
;
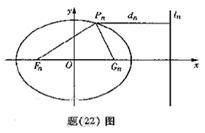 (Ⅱ)取
(Ⅱ)取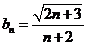 ,并用
,并用 表示
表示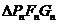 的面积,试证:
的面积,试证: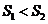 且
且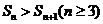
证:(I)由题设及椭圆的几何性质有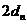
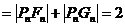 ,故
,故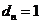 。
。
设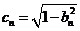 ,则右准线方程为
,则右准线方程为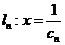 .
.
 因此,由题意
因此,由题意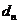 应满足
应满足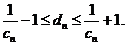 即
即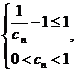 解之得:
解之得: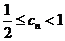 。
。
即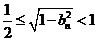 ,从而对任意
,从而对任意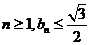 .
.
(II)设点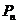 的坐标为
的坐标为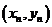 ,则由
,则由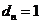 及椭圆方程易知
及椭圆方程易知

 。
。
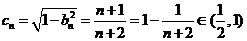
因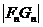
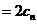 ,故
,故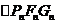 的面积为
的面积为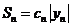 ,
,
从而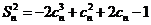 。
。
令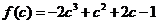 。由
。由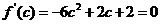 ,得两根
,得两根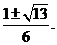 从而易知函数
从而易知函数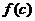 在
在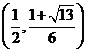 内是增函数。而在
内是增函数。而在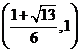 内是减函数。
内是减函数。
现在由题设取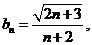 则
则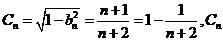 是增数列。
是增数列。
又易知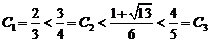 。
。
故由前已证,知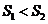 ,且
,且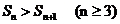 。
。
说明:如果建立Sn与n的函数,讨论单调性比较复杂.
5.2; 6.  +
+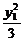 =1,
=1, 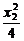 +
+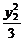 =1.相减得
=1.相减得
∴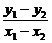 =-
=-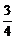 ·
·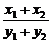 .
.
又∵M为AB中点,x1+x2=2,y1+y2=2.
∴直线l的斜率为-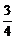 .
.
得直线l的方程为3x+4y-7=0.
4.设左焦点为F1,右焦点为F2,由双曲线定义和三角形边的关系得:

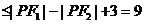 ,选D
,选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com