
3. 已知函数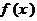 是定义在R上的奇函数,当
是定义在R上的奇函数,当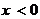 时,
时,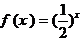 ,则
,则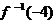 的值是( )
的值是( )
A.2
B.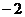 C.3
D.
C.3
D.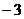
2.若不等式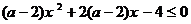 对一切
对一切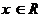 恒成立,则
恒成立,则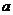 的取值范围是 ( )
的取值范围是 ( )
A.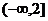 B.
B.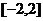 C.
C. D.
D.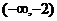
1.已知函数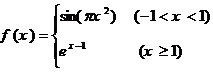 ,若
,若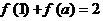 ,则
,则
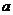 的所有可能值为( )
的所有可能值为( )
A.1
B.1或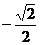 C.
C.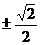 D. 1或
D. 1或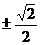
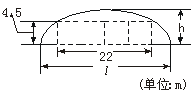
9.(2003上海)如下图,某隧道设计为双向四车道,车道总宽22 m,要求通行车辆限高4.5 m,隧道全长2.5 km,隧道的拱线近似地看成半个椭圆形状.
(1)若最大拱高h为6 m,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6 m,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为S=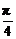 lh,柱体体积为底面积乘以高.本题结果均精确到0.1 m)
lh,柱体体积为底面积乘以高.本题结果均精确到0.1 m)
 (1)解:如下图建立直角坐标系,则点P(11,4.5),
(1)解:如下图建立直角坐标系,则点P(11,4.5),
椭圆方程为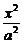 +
+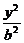 =1.将b=h=6与点P坐标代入椭圆方程,得a=
=1.将b=h=6与点P坐标代入椭圆方程,得a=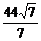 ,此时l=2a=
,此时l=2a=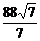 ≈33.3.因此隧道的拱宽约为33.3 m.
≈33.3.因此隧道的拱宽约为33.3 m.
(2)解法一:由椭圆方程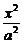 +
+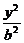 =1,得
=1,得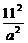 +
+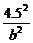 =1.
=1.
因为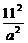 +
+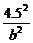 ≥
≥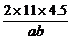 ,即ab≥99,且l=2a,h=b,所以S=
,即ab≥99,且l=2a,h=b,所以S=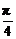 lh=
lh= ≥
≥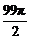 .
.
当S取最小值时,有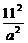 =
=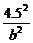 =
=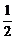 ,
,
得a=11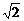 ,b=
,b=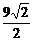 .
.
此时l=2a=22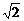 ≈31.1,h=b≈6.4.
≈31.1,h=b≈6.4.
故当拱高约为6.4 m、拱宽约为31.1 m时,土方工程量最小.
解法二:由椭圆方程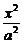 +
+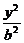 =1,
=1,
得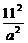 +
+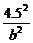 =1.
=1.
于是b2= ·
·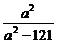 .
.
a2b2= (a2-121+
(a2-121+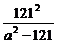 +242)≥
+242)≥ (2
(2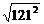 +242)=81×121,
+242)=81×121,
即ab≥99,当S取最小值时,
有a2-121=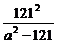 .
.
得a=11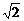 ,b=
,b=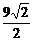 ,以下同解法一.
,以下同解法一.
10
(2006四川)已知两定点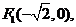
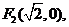 满足条件
满足条件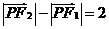 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点 如果
如果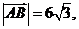 且曲线E上存在点C,使
且曲线E上存在点C,使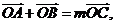 求
求
解:由双曲线的定义可知,曲线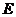 是以
是以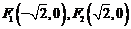 为焦点的双曲线的左支,
为焦点的双曲线的左支,
且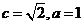 ,易知
,易知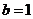
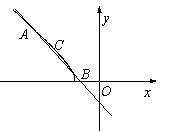 故曲线
故曲线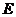 的方程为
的方程为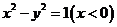
设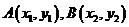 ,由题意建立方程组
,由题意建立方程组
消去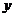 ,得
,得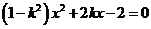
又已知直线与双曲线左支交于两点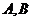 ,有
,有
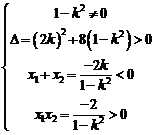 解得
解得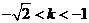
又∵ 
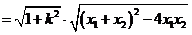
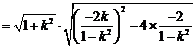
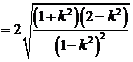
依题意得  整理后得
整理后得 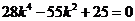
∴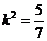 或
或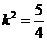 但
但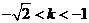 ∴
∴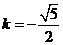
故直线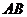 的方程为
的方程为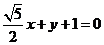
设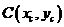 ,由已知
,由已知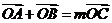 ,得
,得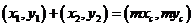
∴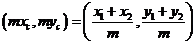 ,
,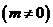
又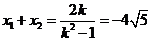 ,
,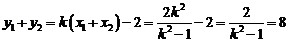
∴点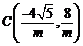
将点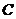 的坐标代入曲线
的坐标代入曲线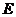 的方程,得
的方程,得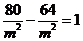
得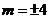 ,但当
,但当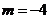 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴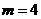 ,
,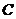 点的坐标为
点的坐标为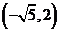
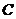 到
到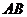 的距离为
的距离为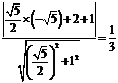
∴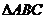 的面积
的面积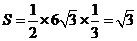
[探索题](2002春全国)已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2,并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1)、C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
(1)求该椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
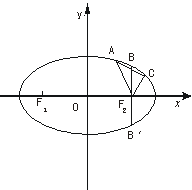
(1)解:由椭圆定义及条件知
2a=|F1B|+|F2B|=10,得a=5.又c=4,
所以b=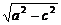 =3.
=3.
故椭圆方程为 +
+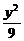 =1.
=1.
(2)解:由点B(4,yB)在椭圆上,得|F2B|=|yB|=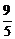 .
.
方法一:因为椭圆右准线方程为x=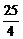 ,离心率为
,离心率为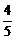 .
.
根据椭圆定义,有|F2A|=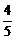 (
(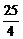 -x1),|F2C|=
-x1),|F2C|=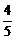 (
(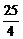 -x2).
-x2).
由|F2A|、|F2B|、|F2C|成等差数列,得
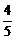 (
(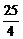 -x1)+
-x1)+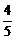 (
(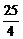 -x2)=2×
-x2)=2×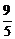 .
.
由此得出x1+x2=8.
设弦AC的中点为P(x0,y0),
则x0=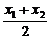 =
=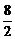 =4.
=4.
方法二:由|F2A|、|F2B|、|F2C|成等差数列,得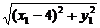 +
+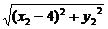 =2×
=2×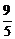 , ①
, ①
由A(x1,y1)在椭圆 +
+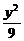 =1上,得
=1上,得
y12=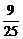 (25-x12),
(25-x12),
所以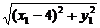
=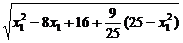
=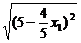 =
=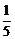 (25-4x1) ②
(25-4x1) ②
同理可得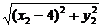 =
=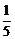 (25-4x2) ③
(25-4x2) ③
将②③代入①式,得
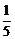 (25-4x1)+
(25-4x1)+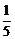 (25-4x2)=
(25-4x2)=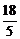 .
.
所以x1+x2=8.
设弦AC的中点为P(x0,y0),
则x0=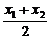 =
=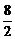 =4.
=4.
(3)解法一:由A(x1,y1),C(x2,y2)在椭圆上,得
9x12+25y12=9×25, ④
9x22+25y22=9×25. ⑤
由④-⑤得9(x12-x22)+25(y12-y22)=0,
即9(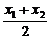 )+25(
)+25(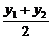 )(
)(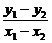 )=0(x1≠x2).
)=0(x1≠x2).
将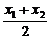 =x0=4,
=x0=4,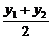 =y0,
=y0,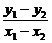 =-
=-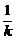 (k≠0)代入上式,得
(k≠0)代入上式,得
9×4+25y0(-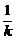 )=0(k≠0).
)=0(k≠0).
由上式得k=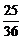 y0(当k=0时也成立).
y0(当k=0时也成立).
由点P(4,y0)在弦AC的垂直平分线上,得
y0=4k+m,
所以m=y0-4k=y0-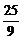 y0=-
y0=- y0.
y0.
由P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,得-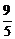 <y0<
<y0<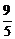 .
.
所以-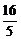 <m<
<m<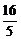 .
.
评述:在推导过程中,未写明“x1≠x2”“k≠0”“k=0时也成立”及把结论写为“-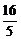 ≤m≤
≤m≤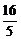 ”也可以.
”也可以.
解法二:因为弦AC的中点为P(4,y0),
所以直线AC的方程为
y-y0=-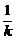 (x-4)(k≠0). ⑥
(x-4)(k≠0). ⑥
将⑥代入椭圆方程 +
+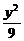 =1,得
=1,得
(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0.
所以x1+x2=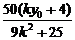 =8.
=8.
解得k=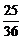 y0(当k=0时也成立).
y0(当k=0时也成立).
以下步骤同解法一.
8.(2005上海文)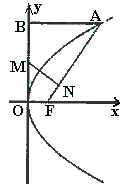 已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于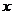 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于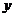 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当K(m.0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
解:(1)抛物线y2=2px的准线为
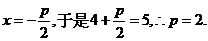
∴抛物线方程为y2= 4x.
(2)∵点A的坐标是(4,4), 由题意得B(0,4),M(0,2),
又∵F(1,0),
∴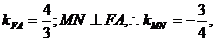
则FA的方程为y=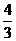 (x-1),MN的方程为
(x-1),MN的方程为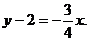
解方程组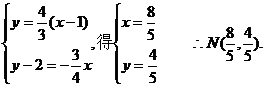
(3)由题意得,圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离,
当m≠4时,直线AK的方程为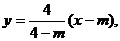 即为
即为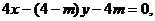
圆心M(0,2)到直线AK的距离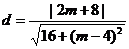 ,令
,令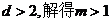
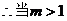 时,直线AK与圆M相离;
时,直线AK与圆M相离;
当m=1时,直线AK与圆M相切;
当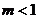 时,直线AK与圆M相交.
时,直线AK与圆M相交.
7.已知椭圆的焦点是F1(-1,0),F2(1,0),P为椭圆上的一点,且|F1F2|是|PF1|和|PF2|的等差中项。(1)求椭圆方程; (2)若点P在第三象限,且∠P F1F2=1200,求tan∠F1PF2。
解:(1)由题设2|F1F2|=|PF1|+|PF2|,c=1。∴2a=4,∴b=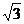 。∴椭圆方程为
。∴椭圆方程为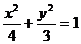 。
。
(2)设∠F1PF2=θ,则∠PF2 F1=600-θ,由正弦定理并结合等比定理可得到

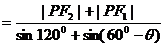 ,
,
∴化简可得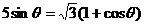 ,∴
,∴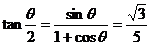 ,
,
从而可求得tan∠F1PF2=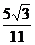 。
。
思维点拨:解与△P F1F2有关的问题(P为椭圆上的点)常用正弦定理或余弦定理,并且结合|PF1|+|PF2|=2a来求解。
6.(2005江西)以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,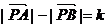 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若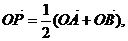 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程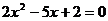 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
简答提示:1-4.DAAD; 5.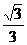 ; 6.③④.
; 6.③④.
[解答题]
5.(2005江苏卷)点P(-3,1)在椭圆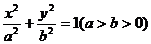 的左准线上,过点P且方向为
的左准线上,过点P且方向为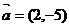 的光线,经直线
的光线,经直线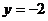 反射后通过椭圆的左焦点,则这个椭圆的离心率为_______
反射后通过椭圆的左焦点,则这个椭圆的离心率为_______
4.(2006湖北)设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若 ,且
,且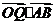 =1,则P点的轨迹方程是( )
=1,则P点的轨迹方程是( )
A. 3x2+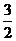 y2=1 (x>0,y>0)
B.3x2-
y2=1 (x>0,y>0)
B.3x2-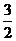 y2=1(x>0, y>0)
y2=1(x>0, y>0)
C.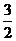 x2-3y2=1(x>0,y>0)
D.
x2-3y2=1(x>0,y>0)
D. 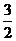 x2+3y2=1(x>0,y>0)
x2+3y2=1(x>0,y>0)
[填空题]
3.(2006辽宁)曲线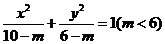 与曲线
与曲线 的 ( )
的 ( )
A.焦距相等 B.离心率相等
C.焦点相同 D.准线相同
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com