
14、根据定义证明函数的单调性时,规范格式是什么?(取值, 作差, 判正负.)可别忘了导数也是判定函数单调性的一种重要方法.在求函数的单调区间或求解不等式时,你知道函数的定义域要优先考虑吗?
例如:(1)函数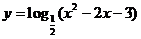 的单调减区间为
的单调减区间为
(2)若函数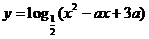 在区间
在区间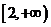 上是减函数,则实数a的取值范围是
上是减函数,则实数a的取值范围是
(3)若定义在R上的偶函数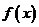 在区间
在区间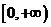 上是单调增函数,则不等式
上是单调增函数,则不等式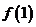
 的解集为
的解集为
13、 判断一个函数的奇偶性时,你注意到函数的定义域是否关于原点对称这个必要非充分条件了吗? 在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数;
例如:(1)函数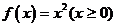 的奇偶性是
的奇偶性是
(2)函数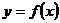 是R上的奇函数,且
是R上的奇函数,且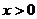 时,
时,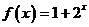 ,则
,则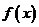 的表达式为
的表达式为
12、你知道求函数值域的常用方法有哪些吗,含参的二次函数的值域、最值要记得讨论.
例如(1)已知函数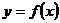 的值域是[
的值域是[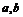 ],则函数
],则函数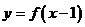 的值域是
的值域是
(2)函数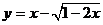 的值域是
的值域是
(3)函数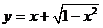 的值域是
的值域是
(4)函数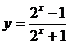 的值域是
的值域是
11、求函数的定义域的常见类型记住了吗?复合函数的定义域弄清了吗?
例如:(1)函数y=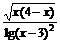 的定义域是 ;
的定义域是 ;
(2)函数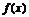 的定义域是[0,1],求
的定义域是[0,1],求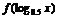 的定义域.
的定义域.
 (3)函数
(3)函数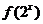 的定义域是(0,1],求
的定义域是(0,1],求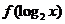 的定义域.
的定义域.
函数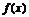 的定义域是[
的定义域是[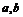 ],
], 求函数
求函数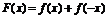 的定义域
的定义域
10、求一个函数的解析式,你标注了该函数的定义域了吗?
例如:(1)若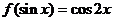 ,则
,则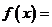
(2)若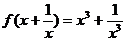 ,则
,则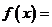
9、函数的几个重要性质:
①如果函数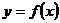 对于一切
对于一切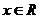 ,都有
,都有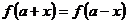 或f(2a-x)=f(x),那么函数
或f(2a-x)=f(x),那么函数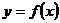 的图象关于直线
的图象关于直线 对称.
对称.
②函数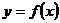 与函数
与函数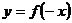 的图象关于直线
的图象关于直线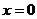 对称;
对称;
函数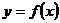 与函数
与函数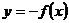 的图象关于直线
的图象关于直线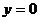 对称;
对称;
函数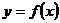 与函数
与函数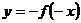 的图象关于坐标原点对称.
的图象关于坐标原点对称.
③若奇函数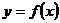 在区间
在区间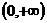 上是递增函数,则
上是递增函数,则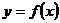 在区间
在区间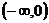 上也是递增函数.
上也是递增函数.
④若偶函数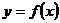 在区间
在区间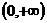 上是递增函数,则
上是递增函数,则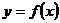 在区间
在区间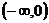 上是递减函数.
上是递减函数.
⑤函数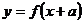
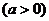 的图象是把函数
的图象是把函数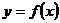 的图象沿x轴向左平移a个单位得到的;函数
的图象沿x轴向左平移a个单位得到的;函数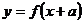 (
(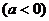 的图象是把函数
的图象是把函数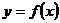 的图象沿x轴向右平移
的图象沿x轴向右平移
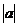 个单位得到的;
个单位得到的;
函数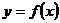 +a
+a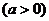 的图象是把函数
的图象是把函数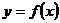 助图象沿y轴向上平移a个单位得到的;函数
助图象沿y轴向上平移a个单位得到的;函数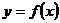 +a
+a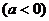 的图象是把函数
的图象是把函数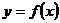 助图象沿y轴向下平移
助图象沿y轴向下平移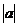 个单位得到的.
个单位得到的.
⑥函数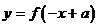 与函数
与函数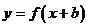 的图象关于直线
的图象关于直线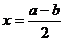 对称
对称
例如:(1)函数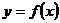 满足
满足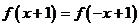 则关于直线
则关于直线
对称
(2)函数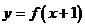 与
与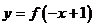 关于直线 对称
关于直线 对称
(3)函数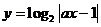 (
(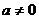 )的图象关于直线
)的图象关于直线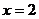 对称,则a=
对称,则a=
(4)函数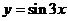 的图象可由
的图象可由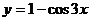 的图象按向量
的图象按向量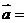 (
(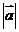 最小)平移得到.
最小)平移得到.
8、你对映射的概念了解了吗?映射f:A→B中,A中元素的任意性和B中与它对应元素的唯一性,映射与函数的关系如何?
例如:函数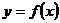 与直线
与直线 的交点的个数有
个
的交点的个数有
个
7. 命题的四种形式及其相互关系;全称命题和存在命题.
(1)原命题与逆否命题同真同假;逆命题与否命题同真同假.
(2)“命题的否定”与“否命题”的区别:____________________
练习:
(1)命题“异面直线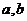 不垂直,则过
不垂直,则过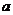 的任一平面与
的任一平面与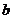 都不垂直”,求出该命题的否命题.
都不垂直”,求出该命题的否命题.
(2)命题“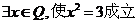 ”,求该命题的否定.
”,求该命题的否定.
 (3)若存在
(3)若存在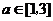 ,使不等式
,使不等式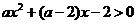 ,求
,求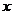 的取值范围.
的取值范围.
6.
两集合之间的关系.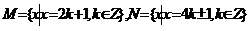
5. 解集合问题的基本工具是韦恩图.
某文艺小组共有10名成员,每人至少会唱歌和跳舞中的一项,其中7人会唱歌跳舞5人会,现从中选出会唱歌和会跳舞的各一人,表演一个唱歌和一个跳舞节目,问有多少种不同的选法?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com