
6.几个重要结论:(1)已知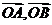 不共线,
不共线,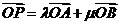 ,则A,P,B三点共线的充要条件是
,则A,P,B三点共线的充要条件是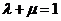 ;(2)向量中点公式:若C是AB的中点,则
;(2)向量中点公式:若C是AB的中点,则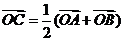 ;(3)向量重心公式:在
;(3)向量重心公式:在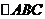 中,
中,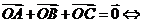
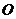 是
是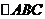 的重心.
的重心.
例:设F为抛物线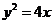 的焦点,A,B,C为该抛物线上三点,若
的焦点,A,B,C为该抛物线上三点,若 ,则
,则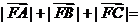 __________.
__________.
5.你还记得向量基本定理的几何意义吗?它的实质就是平面内的任何向量都可以用平面内任意不共线的两个向量线性表示,它的系数的含义与求法你清楚吗?
4.向量的运算要和实数运算有区别:(1)如两边不能约去一个向量,即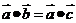 推不出
推不出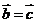 ,(2)向量的乘法不满足结合律,即
,(2)向量的乘法不满足结合律,即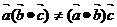 ,(3)两向量不能相除.
,(3)两向量不能相除.
3.利用向量平行或垂直来解决解析几何中的平行和垂直问题可以不用讨论斜率不存在的情况,要注意:
(1)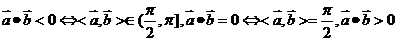
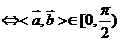
(2)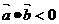 是向量
是向量 夹角为钝角的必要而非充分条件.
夹角为钝角的必要而非充分条件.
2.向量可以解决有关夹角、距离、平行和垂直等问题,要记住以下公式:|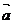 |2=
|2=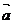 ·
·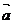 ,
,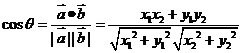
1.两向量平行或共线的条件,它们两种形式表示,你还记得吗?注意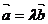 是向量平行的充分不必要条件.(定义及坐标表示)
是向量平行的充分不必要条件.(定义及坐标表示)
10、对于不等式恒成立问题,常用的处理方式?(转化为最值问题)
9、解含参数的不等式的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”
8、 在解含有参数的不等式时,怎样进行讨论?(特别是指数和对数的底
在解含有参数的不等式时,怎样进行讨论?(特别是指数和对数的底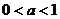 或
或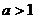 )讨论完之后,要写出:综上所述,原不等式的解集是…….
)讨论完之后,要写出:综上所述,原不等式的解集是…….
7、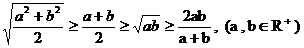 (当且仅当
(当且仅当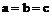 时,取等号); a、b、c
时,取等号); a、b、c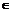 R,
R,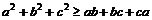 (当且仅当
(当且仅当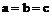 时,取等号);
时,取等号);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com