
8.利用导数证明不等式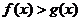 的步骤:
的步骤:
(1)作差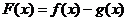 ;
;
(2)判断函数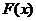 在定义域上的单调性并求它的最小值;
在定义域上的单调性并求它的最小值;
(3)判断最小值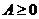 ;
;
(4)结论: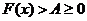 ,则
,则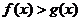 .
.
7.含有参数的函数求最值的方法:
看导数为0的点与定义域之间的关系.
6. 利用导数求最值的步骤:
(1)求函数在给定区间上的极值;
(2)比较区间端点所对的函数值与极值的大小,确定最大值与最小值.
5.求函数极值的方法:
(1)先找定义域,求导数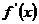 ;
;
 (2)求方程
(2)求方程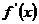 =0的根
=0的根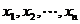 找出定义域的分界点;
找出定义域的分界点;
(3)列表,根据单调性求出极值.
已知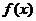 在
在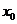 处的极值为A,相当于给出了两个条件:①函数在此点导数值为零,②函数在此点的值为定值.
处的极值为A,相当于给出了两个条件:①函数在此点导数值为零,②函数在此点的值为定值.
4.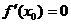 是函数f(x)在x0处取得极值的必要非充分条件,f(x)在x0处取得极值的充分必要条件是什么?
是函数f(x)在x0处取得极值的必要非充分条件,f(x)在x0处取得极值的充分必要条件是什么?
3.
利用导数可以证明或判断函数的单调性,注意当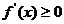 或
或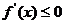 ,带上等号.
,带上等号.
例.已知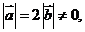 且关于
且关于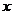 的函数
的函数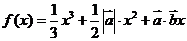 在R上有极值,则
在R上有极值,则 与
与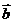 的夹角的范围为
的夹角的范围为
2.几个重要函数的导数:
①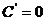 ,(C为常数)
②
,(C为常数)
②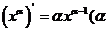 为常数)
为常数)
③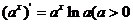 且
且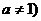 ④
④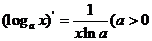 且
且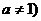
⑤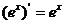 ⑥
⑥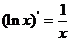
⑦ ⑧
⑧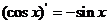
导数的四运算法则
①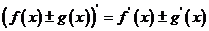
②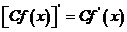 (C为常数)
(C为常数)
③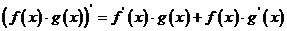
④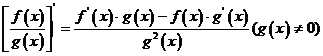
1.导数的几何意义即曲线在该点处的切线的斜率,学会定义的多种变形.
8.一个封闭图形首尾连接而成的向量和为零向量,这是题目中的天然条件,要注意运用,对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以 一个向量,但不能两边同除以一个向量.
例1.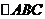 内接于以O为圆心,1为半径的圆,且
内接于以O为圆心,1为半径的圆,且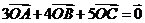 ,求数量积
,求数量积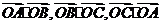 .
.
 例2.平面四边形ABCD中,
例2.平面四边形ABCD中,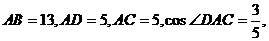
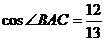 ,设
,设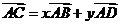 ,求
,求 的值.
的值.
例3.如图,设点O在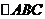 内部,且有
内部,且有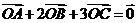 ,则
,则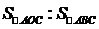 = ____.
= ____.
7.向量等式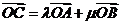 的常见变形方法:(1)两边同时平方;(2)两边同时乘以一个向量;(3)合并成两个新向量间的线性关系.
的常见变形方法:(1)两边同时平方;(2)两边同时乘以一个向量;(3)合并成两个新向量间的线性关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com