
5.独立性检验
(1)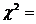 ,
,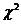 越大说明X与Y
越大说明X与Y
(2)独立性检验的步骤
①假设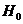
②计算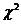
③与临界值比较
④作出推断
4.回归分析:
(1)相关系数
r具有如下性质: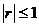 ,并且
,并且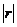 越接近于1,线性相关程度越
越接近于1,线性相关程度越 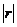 越接近于0,线性相关程度越
越接近于0,线性相关程度越
(2)相关性检验步骤
①提出统计假设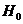 :变量
:变量 不具有相关关系;
不具有相关关系;
②计算出r的值;
③与临界值 比较(
比较( 根据95%的要求与n-2查表可得);
根据95%的要求与n-2查表可得);
④作出统计推断:如果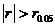 表明
表明
如果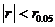 表明
表明
3.线性回归方程:
 步骤:(1)由散点图初步判定是否线性相关;
步骤:(1)由散点图初步判定是否线性相关;
(2)列表求值;
(3)代入计算;
(4)交代结论
2.样本估计总体中:注意频率分布直方图的纵坐标常为频率/组距,小长方形的面积为其频率.总体特征数的估计:
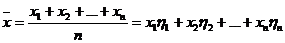 (
(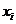 表示各组的组中值,
表示各组的组中值, 表示各组的频率)
表示各组的频率)
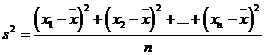
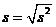
1.抽样方法主要有简单随机抽样(抽签法、随机数表法)常常用于总体数目较少时,主要特征是从总体中逐个抽取;系统抽样,常用于总体个数较多时,主要特征是均衡分成若干部分,每部分只取一个;分层抽样,主要特征是分层按比例抽样,主要使用于总体中有明显差异。它们的共同特征是每个个体被抽到的概率相等。
2.已知在矩形ABCD中,AB=5,AC=7,在矩形内任取一点P,求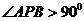 的概率.
的概率.
3.概率题的解题步骤:
(1)记事件
(2)交代总共结果数与A事件中结果数(几何概率即D,d )
(3)计算
(4)作答
例如.1、在等腰直角三角形ABC中,
(1)在斜边AB上任取一点M,求AM小于AC的概率;
(2)过顶点C在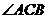 内任作一条射线CM,与线段AB交于点M,求
内任作一条射线CM,与线段AB交于点M,求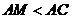 的概率.
的概率.
2.有关某个事件概率的求法:把所求的事件转化为等可能事件的概率,转化为若干个互斥事件中有一个发生的概率,利用对立事件的概率.
(1)若A、B互斥,则P(A+B)=P(A)+P(B);
(2)若A、B对立,则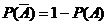 .
.
1.古典概型和几何概型的区别.
例如:(1)任意取实数x [1,100],恰好落在[50,100]之间的概率为
[1,100],恰好落在[50,100]之间的概率为
(2)任意取整数x [1,100],恰好落在[50,100]之间的概率为
[1,100],恰好落在[50,100]之间的概率为
9.利用导数判断方程的解的情况.
.已知函数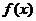 在
在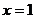 处的导数为1,则当
处的导数为1,则当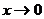 时
时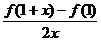 趋近于
趋近于
解析:由定义得当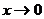 时,
时,
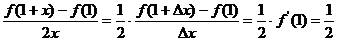
易错原因:不会利用导数的定义来解题.
例2.函数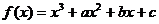 ,其中
,其中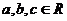 ,当
,当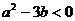 时,
时,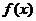 在R上的增减性是
在R上的增减性是
解析: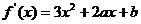 ,则
,则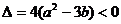 在R上
在R上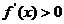 ,故是增函数.
,故是增函数.
易错原因:不善于利用导函数的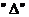 来判别单调性.
来判别单调性.
例3.若函数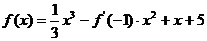 ,则
,则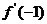 =
=
解析:设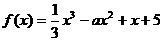 ,则
,则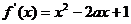 .故
.故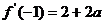 .由
.由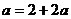 知
知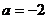 .有
.有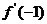 =-2.
=-2.
易错原因:不会运用待定系数法解题.
例4.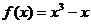 ,则当
,则当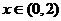 时,
时,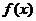 的值域为
的值域为
解析: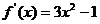 ,令
,令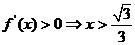 ,
,
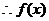 在区间
在区间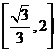 上单调增,在区间
上单调增,在区间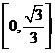 上单调减,
上单调减,

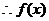 的值域为
的值域为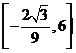 .
.
易错原因:求导之后判别单调区间时概念模糊.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com