

13.在求圆的方程及圆的切线方程时,不妨回忆一下其几何作图方法.尤其是三角形的外接圆、内切圆的作法,两圆内外公切线的作法.
15.在圆中,注意利用半径、半弦长、及弦心距组成的直角三角形并且要更多联想到圆的几何性质.
12.处理圆与圆的位置关系,可用两圆的圆心距与半径之间的关系.
11.过直线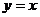 上的一点P向圆C:
上的一点P向圆C: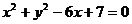 作切线,则切线长的最小值为
作切线,则切线长的最小值为
解析:P点在哪里切线长最小呢?
设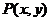 ,切点为A,则在
,切点为A,则在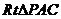 中,
中,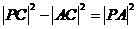
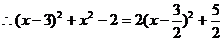
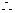 当P在点
当P在点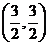 4切线长最小,为
4切线长最小,为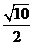 .
.
易错原因:找不到等量关系: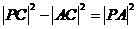 .
.
10.处理直线与圆的位置关系有两种方法:(1)点到直线的距离;(2)直线方程与圆的方程联立,判别式. 一般来说,前者更简捷.
9. 已知两直线分别过(-2,3)和(3,-2),若这两条直线分别绕者这两个点旋转且保持平行,则这两条直线间的距离的取值范围是
已知两直线分别过(-2,3)和(3,-2),若这两条直线分别绕者这两个点旋转且保持平行,则这两条直线间的距离的取值范围是
解析:这两条直线间的距离最大为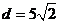 ,则取值范围为
,则取值范围为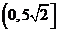
错误原因:未注意“保持平行”.
8.直线的方向向量还记得吗?直线的方向向量与直线的斜率有何关系?当直线L的方向向量为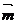 =(x0,y0)时,直线斜率k= ;当直线斜率为k时,直线的方向向量
=(x0,y0)时,直线斜率k= ;当直线斜率为k时,直线的方向向量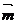 =
=
7.
两直线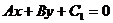 和
和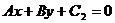 的距离公式d=
的距离公式d=
6.直线在两坐标轴上的截距相等,直线方程可设为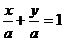 ,但不要忘记当 a=0时,直线y=kx在两条坐标轴上的截距都是0,也是截距相等.
,但不要忘记当 a=0时,直线y=kx在两条坐标轴上的截距都是0,也是截距相等.
5.直线在坐标轴上的截距可正,可负,也可为0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com