
12.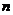 个互斥事件分别发生的概率的和P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
个互斥事件分别发生的概率的和P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
例题:. 由经验得,在某超市的付款处排队等候付款的人数及其概率如下:
|
排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
|
概
率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
求:(1)至多有2个人排队的概率;
(2)至少有2人排队的概率.
解析:(1)设没有人排除为事件A,1个人排队为事件B,2个人排队为事件C,则P(A)=0.1, P(B)=0.16, P(C)=0.3,依题意A、B、C彼此互斥,所以至多2个人排队的概率为:
 P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)设至少2个人排队为事件D,则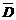 为至多1个人排队,即
为至多1个人排队,即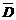 =A+B,因此
=A+B,因此
P(D)=1-P(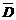 )=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
)=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
11.互斥事件A,B分别发生的概率的和P(A+B)=P(A)+P(B).
10.等可能性事件的概率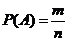 .
.
9.二项式定理 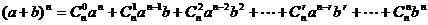 ;
;
二项展开式的通项公式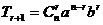
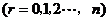 .
.
例题:函数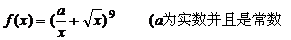 )
)
 (1)已知
(1)已知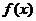 的展开式中
的展开式中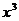 的系数为
的系数为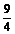 ,求常数
,求常数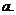
(2)是否存在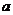 的值,使
的值,使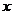 在定义域中取任意值时,
在定义域中取任意值时,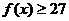 恒成立?如存在,求出
恒成立?如存在,求出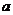 的值,如不存在,说明理由.
的值,如不存在,说明理由.
解析(1)Tr+1=C 由
由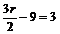 解得
解得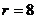
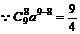
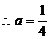
(2)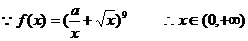 要使(
要使(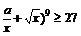
只需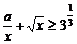
10当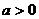 时,设
时,设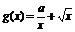
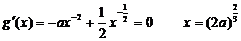
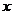 |
(0,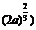 |
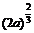 |
(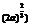 ,+ ,+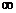 ) ) |
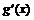 |
- |
0 |
+ |
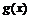 |
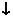 |
极小值 |
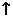 |
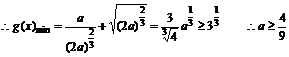
20当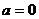 时,不成立 30当
时,不成立 30当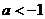 时,不成立 故当
时,不成立 故当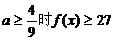
另解法 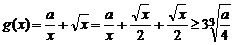 只需
只需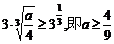
8.排列数与组合数的关系: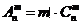 .
.
7.组合恒等式
(1)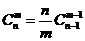 ; (2)
; (2)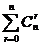 =
=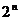 ; (3)
; (3)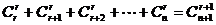 ;
;
(4)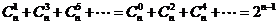
6.组合数的两个性质
(1)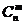 =
=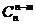 ;(2)
;(2) 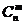 +
+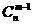 =
= ;注:规定
;注:规定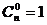 .
.
5.组合数公式
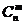 =
=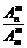 =
=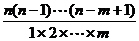 =
=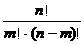 (
(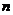 ∈N*,
∈N*,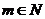 ,且
,且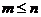 ).
).
4.排列恒等式
(1)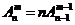 ;(2)
;(2) ;(3)
;(3)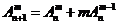 ;
;
(4) 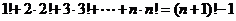 .
.
3.排列数公式
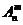 =
=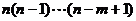 =
=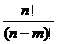 .(
.(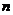 ,
,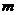 ∈N*,且
∈N*,且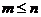 ).注:规定
).注:规定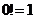 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com