21．(本小题满分12分)

已知函数f(x)=ax³+bx²-x(x∈R，a、b是常数，a≠0)，且当x=1和x=2时，函数f(x)取得极值．

(I)求函数f(x)的解析式；

(Ⅱ)若曲线y=f(x)与g(x)= -3x -m(-2≤x≤0)有两个不同的交点，求实数m的取值范围.

20．(本小题满分12分)

国际上钻石的重量计量单位为克拉．已知某种钻石的价值υ(美元)与其重量ω (克拉)的平方成正比，且一颗重为3克拉的该种钻石的价值为54000美元．

(I)写出υ关于ω的函数关系式；

　 　(Ⅱ)若把一颗钻石切割成重量比为1∶3的两颗钻石，求价值损失的百分率；

　 　(Ⅲ)把一颗钻石切割成两颗钻石，若两颗钻石的重量分别为m克拉和n克拉，试用你所学的数学知识证明：当m=n时，价值损失的百分率最大．

(注：价值损失的百分率=×100%；在切割过程中的重量损耗忽略不计)

19．(本小题满分12分)

如图，在棱长为2的正方体ABCD -A₁B₁C₁D₁中，E、F分别为AA₁，和CC₁的中点．

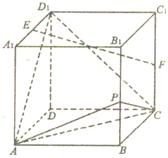(I)求证：EF∥平面ACD，；

(Ⅱ)求异面直线EF与AB所成的角；

(Ⅲ) 设点P在棱BB₁上，且BP=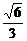求二面角P-AC-B的大小．

18．(本小题满分12分)

在数列中，a₁=1，a_n+1=a_n+c (c为常数，n∈N*)，且a₁，a₂，a₅成公比不等于1的等比数列．

(Ⅰ) 求c的值；

(Ⅱ) 设b_n=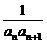，求数列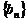的前n项和S_n ．

17．(本小题满分12分)

已知函数f(x)=cos²x+sinxcosx(x∈R)

(I)求f(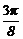)的值；

(Ⅱ)求f(x)的单调递增区间．

15．已知向量a=(1，1)，b=(sinx ，-cosx)，x∈(0，π)，若a∥b ，则x的值是_______．

14．椭圆的焦点及其短轴端点都在以原点为圆心的同一个圆上，则此椭圆的离心率为____．

13．二项式(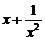)⁶的展开式中，常数项为_____________.

12．若函数f(x)为奇函数，且在(0，+∞)内是增函数，又f(2)=0，则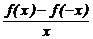＜0的解集为(　　 )

A．(-2,0)∪(0,2)　　　　　　　 B．(-∞，-2)∪(0,2)

C．(-∞，-2)∪(2，+∞)　　　　 D．(-2,0)∪(2，+∞)

第Ⅱ卷(非选择题　 共90分)