
2、已知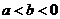 ,则下列不等式一定成立的是
,则下列不等式一定成立的是
A、 B、
B、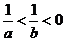 C、
C、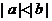 D、
D、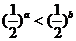
1、已知全集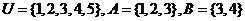 ,则
,则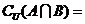
A、{3} B、{4,5} C、{1,2,4,5} D、{1,2,3,4}
16.定义“等和数列”:在一个数列中,如果每一项与它后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做等和数列的公和。已知数列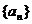 是等和数列,且
是等和数列,且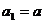 ,公和为
,公和为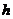 ,则
,则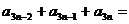 ______;这个数列的前
______;这个数列的前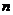 项和
项和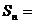 ___;
___;
三:解答题(17~21题,每题12分,第22题14分,共计74分)
17:已知在锐角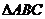 中,角
中,角 的对边分别为
的对边分别为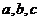 且
且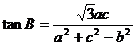 ;
;
(1)求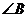 ;
;
(2)求函数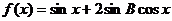 ,
,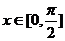 的周期及单调递减区间;
的周期及单调递减区间;
18:在正三棱柱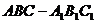 的所有棱长均为
的所有棱长均为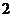 ,
,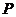 是侧棱
是侧棱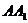 上任意一点,
上任意一点,
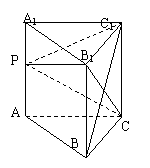 (1)判断直线
(1)判断直线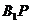 与平面
与平面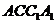 是否垂直,请证明你的结论;
是否垂直,请证明你的结论;
(2)当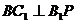 时,求二面角
时,求二面角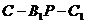 的余弦值;
的余弦值;
19:.某市环保所对市中心每天环境污染情况进行调查研究后,得出一天中环境综合污染指数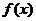 与时间
与时间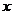 (小时)的关系为
(小时)的关系为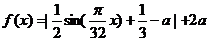 ,
, ,
,
其中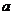 为与气象有关的参数,且
为与气象有关的参数,且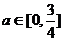 ,若用每天
,若用每天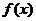 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作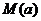 ;
;
(1) 令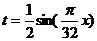 ,
, ,求
,求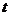 的取值范围;
的取值范围;
(2) 求函数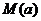 ;
;
(3) 为加强对环境污染的整治,市政府规定每天的综合污染指数不得超过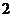 ,试问目前市中心的综合污染指数是多少?是否超标?
,试问目前市中心的综合污染指数是多少?是否超标?
20:已知函数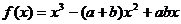 ,这里
,这里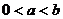 ;
;
(1)设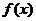 在
在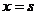 与
与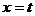 处取得极值,其中
处取得极值,其中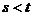 ,求证:
,求证: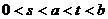 ;
;
(2)设点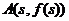 ,
, ,求证:线段
,求证:线段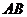 的中点
的中点 在曲线
在曲线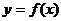 上;
上;
21:观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
… … … …
… … … … …
假设第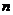 行的第二个数为
行的第二个数为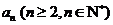 ,
,
(Ⅰ)依次写出第六行的所有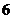 个数字;
个数字;
(Ⅱ)归纳出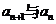 的关系式并求出
的关系式并求出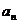 的通项公式;
的通项公式;
(Ⅲ)设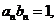 求证:
求证: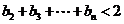
22:已知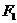 、
、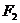 分别是椭圆
分别是椭圆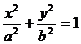
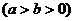 的左、右焦点,右焦点
的左、右焦点,右焦点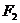 到上顶点的距离为
到上顶点的距离为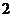 ,右准线
,右准线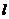 :
: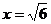 ;
;
(1)求此椭圆的方程;
(2)点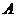 是椭圆的右顶点,直线
是椭圆的右顶点,直线 与椭圆交于
与椭圆交于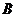 、
、 两点(
两点( 在第一象限内),又
在第一象限内),又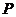 、
、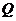 是此椭圆上两点,并且满足
是此椭圆上两点,并且满足 ,求证:向量
,求证:向量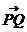 与
与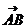 共线
共线
15.设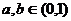 ,则关于
,则关于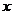 的方程
的方程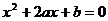 在
在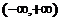 上有两个零点的概率为_______ ;
上有两个零点的概率为_______ ;
14.如图,是一个程序框图,
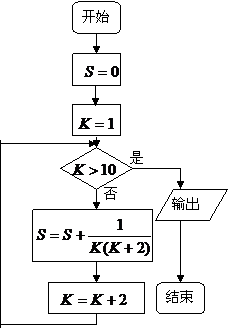 则输出结果为____________
则输出结果为____________
13.已知向量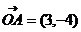 ,
,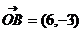 ,
,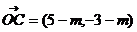 ,若点A、B、C三点能构成三角形,则实数
,若点A、B、C三点能构成三角形,则实数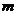 应满足的条件是__________ ;
应满足的条件是__________ ;
12. 不等式组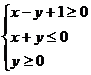 表示的平面区域的面积是_______;
表示的平面区域的面积是_______;
11.函数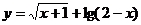 的定义域__________;
的定义域__________;
10.定义:设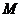 是非空实数集,若
是非空实数集,若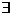
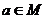 ,使得对于
,使得对于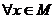 ,都有
,都有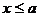
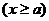 ,
,
则称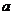 是
是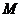 的最大(小)值,若
的最大(小)值,若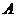 是一个不含零的非空实数集,且
是一个不含零的非空实数集,且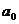 是
是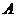 的最大值,则( )
的最大值,则( )
A. 当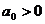 时,
时,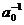 是集合
是集合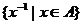 的最小值;
的最小值;
B. 当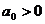 时,
时,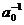 是集合
是集合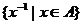 的最大值;
的最大值;
C. 当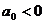 时,
时,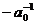 是集合
是集合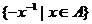 的最小值;
的最小值;
D. 当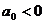 时,
时,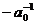 是集合
是集合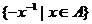 的最大值;
的最大值;
二:填空题(每小题4分 ,共16分)
9. 若函数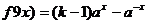
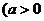 且
且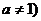 在
在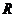 上既是奇函数,又是偶函数,则
上既是奇函数,又是偶函数,则
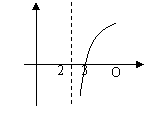
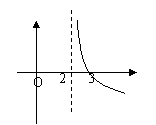

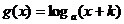 的图像是( A )
的图像是( A )
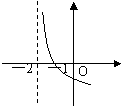
A B C D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com