
22、设三次函数 ,在
,在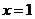 处取得极值,其图像在
处取得极值,其图像在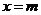 处的切线的斜率为
处的切线的斜率为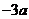 。
。
(1)求证: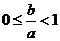 ;
;
(2)若函数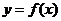 在区间
在区间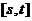 上单调递增,求
上单调递增,求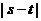 的取值范围;
的取值范围;
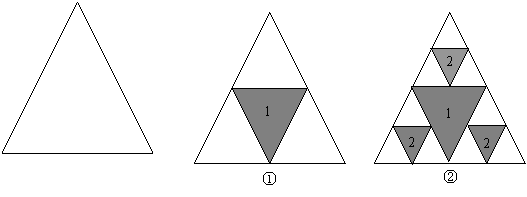
21、如图是一个面积为1的三角形,现进行如下操作。第一次操作:分别连接这个三角形三边的中点,构成4个三角形,挖去中间一个三角形(如图①中阴影部分所示),并在挖去的三角形上贴上数字标签“1”;第二次操作:连结剩余的三个三角形三边的中点,再挖去各自中间的三角形(如图②中阴影部分所示),同时在挖去的3个三角形上都贴上数字标签“2”;第三次操作:连接剩余的各三角形三边的中点,再挖去各自中间的三角形,同时在挖去的三角形上都贴上数字标签“3”;……,如此下去,记第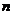 次操作后剩余图形的总面积为
次操作后剩余图形的总面积为
(1)求 ;
;
(2)求第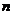 次操作后,挖去的所有三角形上所贴标签上的数字和
次操作后,挖去的所有三角形上所贴标签上的数字和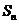 ;
;
20、函数f(x)=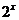 ,g(x)=
,g(x)=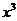 的图象的示意图如图所示,
的图象的示意图如图所示,
设两函数的图象交于点A(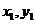 )B(
)B(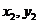 ),且
),且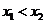
(1)
请指出示意图中曲线C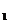 ,C
,C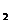 分别对应哪一个函数?
分别对应哪一个函数?
(2)
若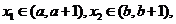 且
且
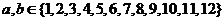 ,指出a,b的值,
,指出a,b的值,
并说明理由;
(3)
|
g(2009)的大小
19、某教研机构准备举行一次高中数学新课程研讨会,拟邀请50名使用不同版本的一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
10 |
5 |
(1)假设使用北师大版的5名教师中有3名男教师,2名女教师,若随机选出2名用北师大版的教师发言,求恰好是一男一女的概率P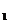
(3)
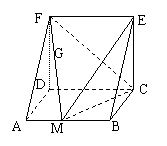
从这50名教师中随机选出2名教师发言,求第一位发言的教师所使用版本是北师大版的概率P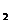
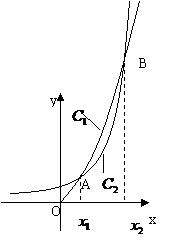
18、一个多面体的直观图和三视图如图所示,其中M、G分别是AB、DF的中点。
(1) 在AD上(含A、D端点)确定一点P,使得GP//平面FMC;
(2) 一只苍蝇在几何体ADF-BCE内自由飞翔,求它飞入几何体F-AMCD内的概率。

17、已知函数f(x)=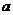 sinx+bcosx的图象经过点(
sinx+bcosx的图象经过点(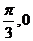 ),(
),(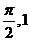 )
)
(1) 求实数a和b的值;
(2) 当x为何值时,f(x)取得最大值。
16、函数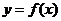 是定义在
是定义在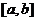 上的增函数,其中
上的增函数,其中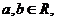 且
且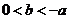 ,已知
,已知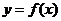 无零点,设函数
无零点,设函数 ,则对于
,则对于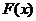 有以下四个说法:
有以下四个说法:
①定义域是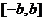 ;②是偶函数;③最小值是0;④在定义域内单调递增。
;②是偶函数;③最小值是0;④在定义域内单调递增。
其中正确的有_____________(填入你认为正确的所有序号)
15、已知函数 ,则
,则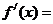 _______.
_______.
14、青年歌手大奖赛共有10名选手参赛,并请了
7名评委,如图的精液图是7名评委给参加最后决
赛的两位选手甲、乙评定的成绩,则乙选手的成绩
中众数出现的频率是_________.
13、 计算
计算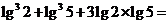 __________
__________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com