
4、某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为 .
.
(Ⅰ)求比赛三局甲获胜的概率;
(Ⅱ)求甲获胜的概率;
(Ⅲ)设甲比赛的次数为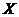 ,求
,求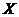 的数学期望.
的数学期望.
扬州市2008-2009学年度第一学期期未调研测试试题
3、如图,四棱锥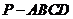 中,底面ABCD是矩形,
中,底面ABCD是矩形,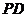 ⊥平面ABCD,且
⊥平面ABCD,且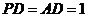 ,
,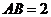 ,点E是AB上一点,AE等于何值时,二面角
,点E是AB上一点,AE等于何值时,二面角 的平面角为
的平面角为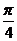 .
.
2、选修4-4 参数方程与极坐标
已知某圆锥曲线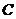 的参数方程为
的参数方程为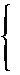
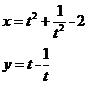 (
(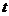 为参数).
为参数).
(Ⅰ)试将圆锥曲线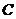 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)以圆锥曲线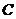 的焦点为极点,以它的对称轴为极轴建立极坐标系,试求它的极坐标方程.
的焦点为极点,以它的对称轴为极轴建立极坐标系,试求它的极坐标方程.
(总分40分,加试时间30分钟)
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内.解答过程应写在答题卷的相应位置上,在其它地方答题无效。
1、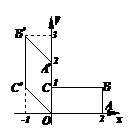 选修4-2 矩阵与变换
选修4-2 矩阵与变换
如图矩形 在变换
在变换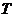 的作用下变成了平行四边形
的作用下变成了平行四边形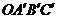 ,求变换
,求变换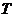 所对应的矩阵
所对应的矩阵 .
.
20.(本题满分16分)
已知等差数列 的首项为
的首项为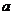 ,公差为
,公差为 ,等比数列
,等比数列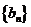 的首项为
的首项为 ,公比为
,公比为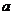 (其中
(其中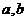 均为正整数).
均为正整数).
(Ⅰ) 若 ,求数列
,求数列 、
、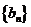 的通项公式;
的通项公式;
(Ⅱ)在(Ⅰ)的条件下,若
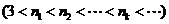 成等比数列,求数列
成等比数列,求数列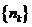 的通项公式;
的通项公式;
(Ⅲ) 若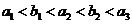 ,且至少存在三个不同的
,且至少存在三个不同的 值使得等式
值使得等式 成立,试求
成立,试求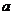 、
、 的值.
的值.
扬州市2008-2009学年度第一学期期未调研测试试题
高 三 数 学
19.(本小题满分16分)
已知函数 .
.
(Ⅰ)若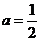 ,求
,求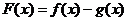 的单调区间;
的单调区间;
(Ⅱ)若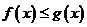 恒成立,求
恒成立,求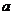 的取值范围.
的取值范围.
18、(本题满分15分)
已知圆 交
交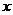 轴于
轴于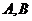 两点,曲线
两点,曲线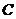 是以
是以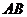 为长轴,直线
为长轴,直线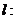
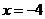 为准线的椭圆.
为准线的椭圆.
(Ⅰ)求椭圆的标准方程;
 (Ⅱ)若
(Ⅱ)若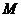 是直线
是直线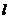 上的任意一点,以
上的任意一点,以 为直径的圆
为直径的圆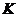 与圆
与圆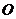 相交于
相交于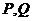 两点,求证:直线
两点,求证:直线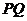 必过定点
必过定点 ,并求出点
,并求出点 的坐标;
的坐标;
(Ⅲ)如图所示,若直线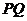 与椭圆
与椭圆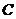 交于
交于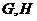 两点,且
两点,且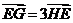 ,试求此时弦
,试求此时弦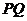 的长.
的长.
17、(本题满分15分)
为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议。现对他前7次考试的数学成绩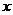 、物理成绩
、物理成绩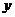 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.
|
数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
|
物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(Ⅱ)已知该生的物理成绩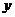 与数学成绩
与数学成绩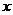 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
16.(本题满分14分)
在正方体 中,
中,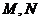 分别是
分别是 中点.
中点.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面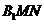 ⊥平面
⊥平面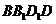 ;
;
(Ⅱ)若在棱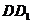 上有一点
上有一点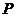 ,使
,使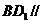 平面
平面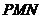 ,求
,求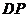 与
与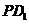 的比.
的比.
15.(本题满分14分)
在△ABC中,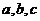 分别是角A,B,C的对边,
分别是角A,B,C的对边,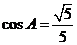 ,
,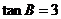 .
.
(Ⅰ)求角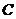 的值;
的值;
(Ⅱ)若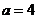 ,求△ABC面积.
,求△ABC面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com