
3.解法一:
 (1)证明:作
(1)证明:作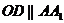 交
交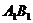 于
于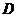 ,连
,连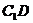 .
.
则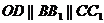 .
.
因为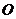 是
是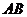 的中点,
的中点,
所以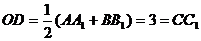 .
.
则 是平行四边形,因此有
是平行四边形,因此有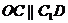 .
.
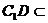 平面
平面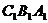 且
且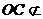 平面
平面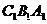 ,
,
则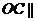 面
面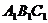 .……………….5分
.……………….5分
(2)如图,过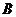 作截面
作截面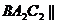 面
面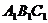 ,分别交
,分别交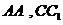 于
于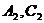 .
.
作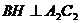 于
于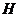 ,连
,连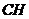 .
.
因为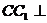 面
面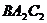 ,所以
,所以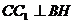 ,则
,则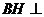 平面
平面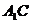 .
.
又因为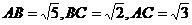
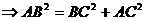 .
.
所以 ,根据三垂线定理知
,根据三垂线定理知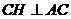 ,所以
,所以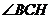 就是所求二面角的平面角.
就是所求二面角的平面角.
因为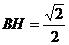 ,所以
,所以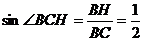 ,故
,故 ,
,
即:所求二面角的大小为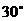 .……………….10分
.……………….10分
解法二:
(1)如图,以 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
 则
则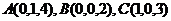 因为
因为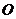 是
是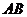 的中点,所以
的中点,所以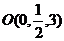 ,
,
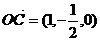 .
.
易知,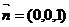 是平面
是平面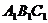 的一个法向量.
的一个法向量.
因为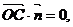
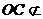 平面
平面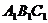 ,
,
所以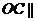 平面
平面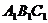 .……………….5分
.……………….5分
(2)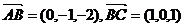 ,
,
设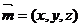 是平面
是平面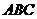 的一个法向量,则
的一个法向量,则
则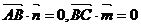 得:
得: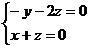
取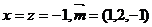 .
.
显然,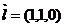 为平面
为平面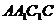 的一个法向量.
的一个法向量.
则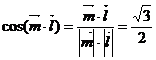 ,结合图形可知所求二面角为锐角.
,结合图形可知所求二面角为锐角.
所以二面角 的大小是
的大小是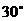 .……………….10分
.……………….10分
4.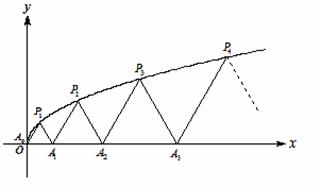 (本题满分10分)如图,
(本题满分10分)如图, 、
、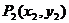 、…、
、…、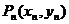
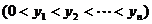 是曲线
是曲线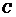 :
: 上的
上的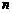 个点,点
个点,点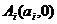 (
(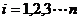 )在
)在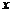 轴的正半轴上,且
轴的正半轴上,且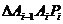 是正三角形(
是正三角形(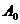 是坐标原点).
是坐标原点).
(Ⅰ)写出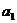 、
、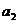 、
、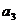 ;
;
(Ⅱ)求出点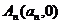 (
(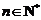 )的
)的
横坐标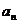 关于
关于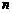 的表达式并证明.
的表达式并证明.
1解:以有点为原点,极轴为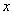 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)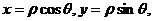 由
由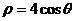 得
得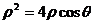 .
.
所以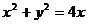 .
.
即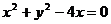 为圆
为圆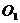 的直角坐标方程.……………….3分
的直角坐标方程.……………….3分
同理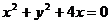 为圆
为圆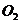 的直角坐标方程.……………….6分
的直角坐标方程.……………….6分
(2)由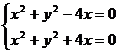 解得
解得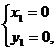
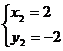 .
.
即圆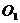 ,圆
,圆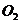 交于点
交于点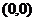 和
和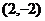 .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为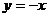 .……………….10分
.……………….10分
2解:分别记甲、乙、丙经第一次烧制后合格为事件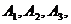
(1)设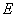 表示第一次烧制后恰好有一件合格,则
表示第一次烧制后恰好有一件合格,则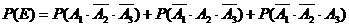
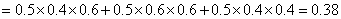 .……………….5分
.……………….5分
(2)解法一:因为每件工艺品经过两次烧制后合格的概率均为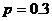 ,
,
所以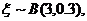
故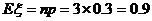 .……………….10分
.……………….10分
解法二:分别记甲、乙、丙经过两次烧制后合格为事件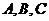 ,
,
则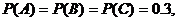
所以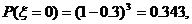
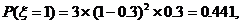
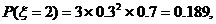
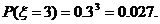
于是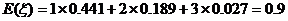 ……………….10分
……………….10分
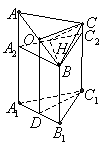
3.(本小题满分10分)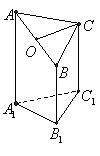 右图是一个直三棱柱(以
右图是一个直三棱柱(以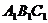 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为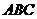 .已知
.已知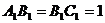 ,
,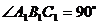 ,
,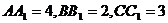 .
.
(1)设点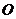 是
是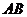 的中点,证明:
的中点,证明: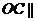 平面
平面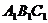 ;
;
(2)求二面角 的大小;
的大小;
2. (本题10分)某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为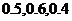 ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为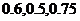 .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为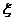 ,求随机变量
,求随机变量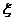 的期望.
的期望.
1. (本题10分)圆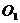
 和圆
和圆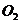 的极坐标方程分别为
的极坐标方程分别为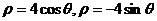 .
.
(1)把圆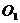
 和圆
和圆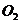 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过圆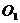
 ,圆
,圆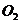 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
20.解 (1)数列
(1)数列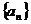 是公差为
是公差为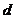
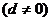 的等差数列
的等差数列
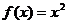 ,且
,且
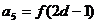
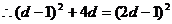
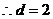
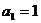
 ………………….4分
………………….4分
数列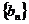 是公比为
是公比为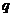 的(q∈R)的等比数列
的(q∈R)的等比数列
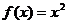 ,且,
,且,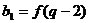 ,
,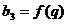
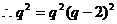
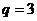
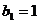
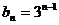 ………………….8分
………………….8分
(2) 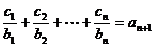
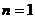
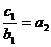
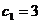 ,
,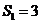 ………………….10分
………………….10分
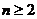
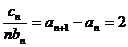
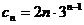 ………………….12分
………………….12分

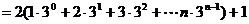
设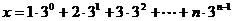

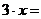
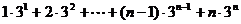
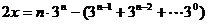
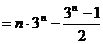
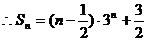 ………………….14分
………………….14分
 综上
综上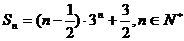 ………………….16分
………………….16分
 泰州实验中学2008-2009学年度第一学期期末考试
泰州实验中学2008-2009学年度第一学期期末考试
高三数学理科附加题 命题人:毛加和
本卷共有4题,解答下列各题必须写出必要的步骤,每题10分.
19、[解](1)当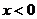 时
时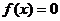 ,当
,当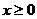 时,
时,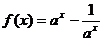 . …………….2分
. …………….2分
由条件可知,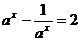 ,即
,即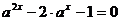 解得
解得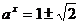 …………6分
…………6分
∵ 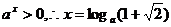 …………..8分
…………..8分
(2)当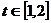 时,
时,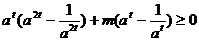 ……………10分
……………10分
即 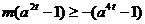
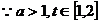
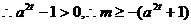 ………………13分
………………13分
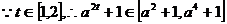
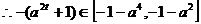
故m的取值范围是 …………….16分
…………….16分
17. .解: (1)
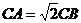 ,
,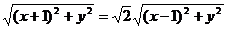
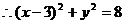 ………………….8分
………………….8分
(2)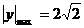 ………………….10分
………………….10分
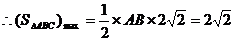 ………………….15分
………………….15分
18解 (1)由表中数据,知
(1)由表中数据,知 ,
, 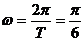
 由
由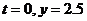 得
得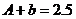
由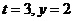 ,得
,得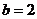

所以,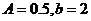 振幅A=
振幅A=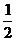 ,∴y=
,∴y=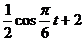 ………………….8分
………………….8分
(2)由题意知,当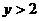 时,才可对冲浪者开放
时,才可对冲浪者开放 ∴
∴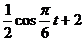 >2,
>2, 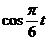 >0
>0
∴–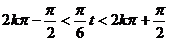 ,
,
即有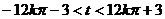 ,
,
由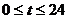 ,故可令
,故可令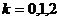 ,得
,得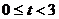 或
或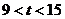 或
或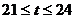
 ……1.4分
……1.4分
∴在规定时间内有6个小时可供游泳爱好者运动即上午9 00至下午15
00至下午15 00
00 ……….15分
……….15分
16.解:(1)取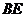 的中点为
的中点为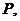 连
连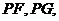 可以证明
可以证明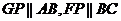
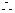 面
面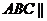 面
面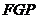 ,
, 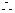
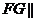 面
面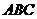 …………………6分
…………………6分
(2)取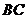 中点
中点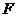 ,连接
,连接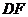 交
交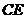 于点
于点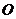 ,
,
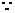
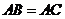 ,
,
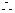
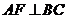 ,
,
又面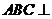 面
面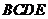 ,
,
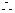
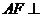 面
面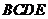 ,
,
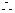
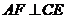 .………………….10分
.………………….10分
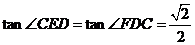 ,
,
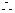
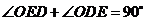 ,
,
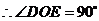 ,即
,即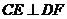 ,
,
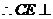 面
面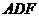 ,
,
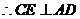 .………………….14分
.………………….14分
15.解:(1)由 得
得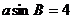 ,
,
由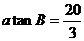 与
与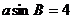 两式相除,有:
两式相除,有:
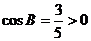 ,
, ………………….4分
………………….4分
又通过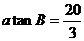 知:
知: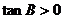 ,
,
则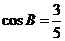 ,
,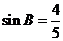 ,
,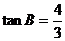
则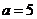 .
. ………………….8分
………………….8分
(2)由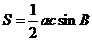 ,得到
,得到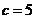 .
.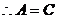
 ………………….10分
………………….10分
由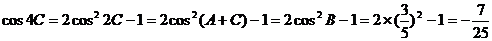
 ….14分
….14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com