
5.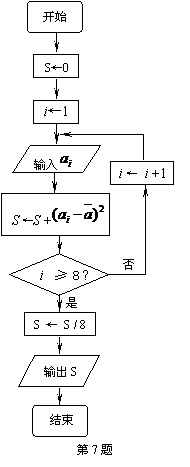 某单位为了了解用电量y度与气温
某单位为了了解用电量y度与气温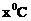 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
|
气温(0C) |
18 |
13 |
10 |
-1 |
|
用电量(度) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程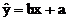 中
中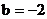 ,预测当气温为
,预测当气温为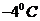
时,用电量的度数约为____▲____.
4.设不等式组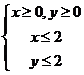 所表示的区域为
所表示的区域为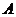 ,现在区域
,现在区域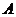 中任意丢进一个粒子,则该粒子落在直线
中任意丢进一个粒子,则该粒子落在直线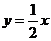 上方的概率为____▲____.
上方的概率为____▲____.
3.如图,一个几何体的主视图与左视图都是边长为2的正方形,其俯视图是直径为2的圆,则该几何体的表面积为____▲____.
2.设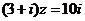 (
(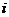 为虚数单位),则
为虚数单位),则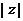 =____▲____.
=____▲____.
1.已知角 的终边过点
的终边过点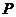 (-5,12),则
(-5,12),则 =____▲____.
=____▲____.
23.(1)根据分步计数原理,摆放鲜花的不同方案有: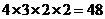 种.……………………2分
种.……………………2分
(2)① 设M表示事件“恰有两个区域用红色鲜花”,
如图二,当区域A、D同色时,共有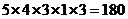 种;
种;
当区域A、D不同色时,共有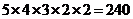 种;
种;
因此,所有基本事件总数为:180+240=420种.……………………………………………4分
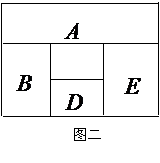 (由于只有A、D,B、E可能同色,故可按选用3色、4色、
(由于只有A、D,B、E可能同色,故可按选用3色、4色、
5色分类计算,求出基本事件总数为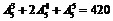 种)
种)
它们是等可能的。又因为A、D为红色时,共有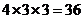 种;
种;
B、E为红色时,共有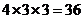 种;
种;
因此,事件M包含的基本事件有:36+36=72种.
所以,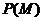 =
=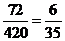 . ……………………………………………………………6分
. ……………………………………………………………6分
②随机变量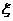 的分布列为:
的分布列为:
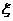 |
0 |
1 |
2 |
|
P |
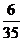 |
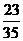 |
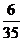 |
所以,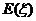 =
=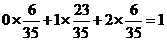 .……………………………………………………10分
.……………………………………………………10分
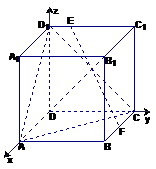
22.设正方体棱长为1,以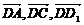 为单位正交基底,建立如图所示坐标系
为单位正交基底,建立如图所示坐标系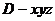 ,则各点的坐标分别为
,则各点的坐标分别为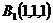 ,
, ,
, 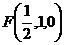 ,………………………………………………2分
,………………………………………………2分
 所以
所以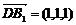 ,
,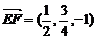 , ……………………4分
, ……………………4分
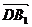 为平面
为平面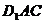 的法向量,
的法向量,
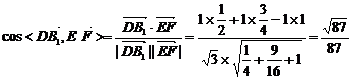 .……8分
.……8分
所以直线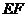 与平面
与平面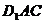 所成角的正弦值为
所成角的正弦值为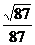 .………………………………………………10分
.………………………………………………10分
21.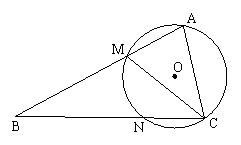 A 证明:如图,在△ABC中,因为CM是∠ACM的平分线,
A 证明:如图,在△ABC中,因为CM是∠ACM的平分线,
所以 .又已知
.又已知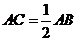 ,
,
所以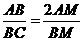 …①…………………… 4分
…①…………………… 4分
又因为BA与BC是圆O过同一点B的弦,
所以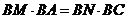 ,即
,即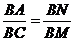 ……② ………………………………8分
……② ………………………………8分
由①、②可知,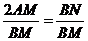 ,所以BN=2AM.
………………………………10分
,所以BN=2AM.
………………………………10分
B 取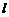 上两点(0,7)和(3.5,0),
…………………………………………………………2分
上两点(0,7)和(3.5,0),
…………………………………………………………2分
则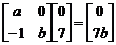 ,
,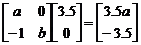 , ………………………………………6分
, ………………………………………6分
由题意知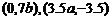 在直线
在直线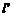 :9x+y-91=0上,
:9x+y-91=0上,
∴ …………………………………………………………………………8分
…………………………………………………………………………8分
解得 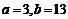 …………………………………………………………………………10分
…………………………………………………………………………10分
C (1)消去参数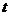 ,得直线
,得直线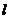 的直角坐标方程为
的直角坐标方程为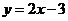 ; ………………………………4分
; ………………………………4分
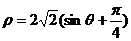 ,即
,即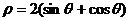 ,两边同乘以
,两边同乘以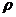 得
得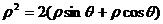 ,
,
消去参数 ,得⊙
,得⊙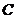 的直角坐标方程为:
的直角坐标方程为: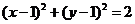 ………………………8分
………………………8分
(2)圆心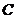 到直线
到直线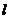 的距离
的距离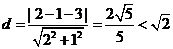 ,所以直线
,所以直线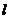 和⊙
和⊙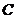 相交.…………10分
相交.…………10分
D 因为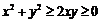 ………………………………………………………2分
………………………………………………………2分
所以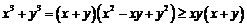 …………………………………………………4分
…………………………………………………4分
同理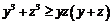 ,
,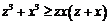 …………………………………………………8分
…………………………………………………8分
三式相加即可得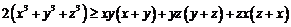
又因为
所以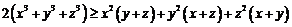 ………………………………………10分
………………………………………10分
20.(1)当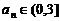 时,则
时,则
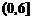 ,当
,当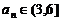 时,则
时,则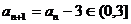 ,
,
故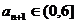 ,所以当
,所以当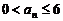 时,总有
时,总有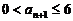 . ……………………………………4分
. ……………………………………4分
(2)①当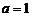 时,
时,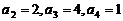 ,故满足题意的
,故满足题意的 N*.
N*.
同理可得,当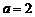 或4时,满足题意的
或4时,满足题意的 N*.
N*.
当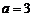 或6时,满足题意的
或6时,满足题意的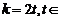 N*.
N*.
②当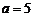 时,
时,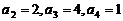 ,故满足题意的k不存在.
,故满足题意的k不存在.
③当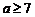 时,由(1)知,满足题意的k不存在.
时,由(1)知,满足题意的k不存在.
综上得:当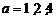 时,满足题意的
时,满足题意的 N*;
N*;
当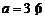 时,满足题意的
时,满足题意的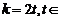 N*. ………………………………………10分
N*. ………………………………………10分
(3)由m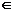 N*,可得
N*,可得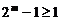 ,故
,故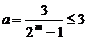 ,
,
当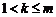 时,
时,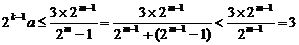 .
.
故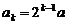 且
且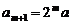 .又
.又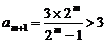 ,
,
所以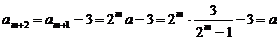 .
.
故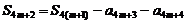
=4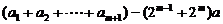
=4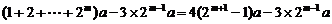
=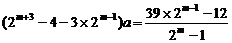 . ………………………………………16分
. ………………………………………16分
附加试题
19.(1)当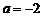 时,
时,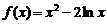 ,当
,当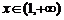 ,
,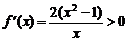 ,
,
故函数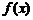 在
在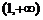 上是增函数.…………………………………………………………………4分
上是增函数.…………………………………………………………………4分
(2)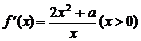 ,当
,当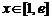 ,
,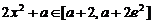 .
.
若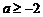 ,
,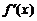 在
在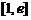 上非负(仅当
上非负(仅当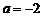 ,x=1时,
,x=1时, ),故函数
),故函数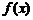 在
在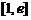 上是增函数,此时
上是增函数,此时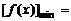
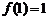 . ……………………………………………………………6分
. ……………………………………………………………6分
若 ,当
,当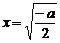 时,
时, ;当
;当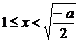 时,
时,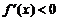 ,此时
,此时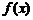
是减函数; 当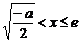 时,
时,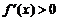 ,此时
,此时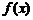 是增函数.故
是增函数.故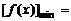
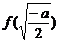
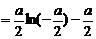 .
.
若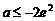 ,
,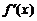 在
在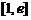 上非正(仅当
上非正(仅当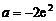 ,x=e时,
,x=e时, ),故函数
),故函数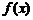 在
在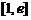 上是减函数,此时
上是减函数,此时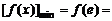
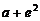 .………………………………………………………8分
.………………………………………………………8分
综上可知,当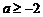 时,
时,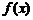 的最小值为1,相应的x值为1;当
的最小值为1,相应的x值为1;当 时,
时,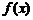
的最小值为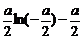 ,相应的x值为
,相应的x值为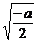 ;当
;当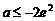 时,
时,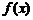 的最小值为
的最小值为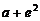 ,
,
相应的x值为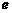 .……………………………………………………………………………………10分
.……………………………………………………………………………………10分
(3)不等式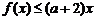 , 可化为
, 可化为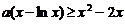 .
.
∵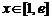 , ∴
, ∴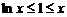 且等号不能同时取,所以
且等号不能同时取,所以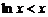 ,即
,即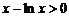 ,
,
因而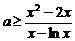 (
(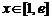 )…………………………………………………………………………12分
)…………………………………………………………………………12分
令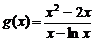 (
(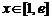 ),又
),又 ,………………………………14分
,………………………………14分
当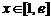 时,
时,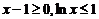 ,
,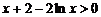 ,
,
从而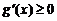 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以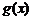 在
在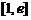 上为增函数,
上为增函数,
故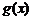 的最小值为
的最小值为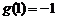 ,所以a的取值范围是
,所以a的取值范围是 . …………………………………16分
. …………………………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com