
20、 (本大题满分12分)
已知数列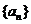 满足:
满足: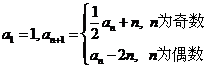 ,且
,且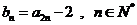
(Ⅰ)求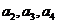 ;
;
(Ⅱ)求证数列 为等比数列并求其通项公式;
为等比数列并求其通项公式;
(Ⅲ)(理)求和S2n+1=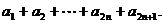
(文)求和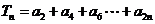
19、(本大题满分12分)
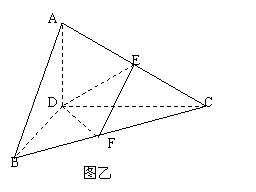
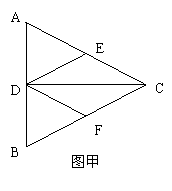
如图甲正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,先将△ABC沿CD折叠成直二面角A-DC-B(如图乙),在乙图中
(Ⅰ)求二面角E-DF-C的余弦值;
(Ⅱ)在线段BC上找一点P,使AP⊥DE,并求BP.
(Ⅲ)求三棱锥D-ABC外接球的表面积.(只需用数字回答,可不写过程)
18、(本大题满分12分)
(理)四个纪念币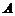 、
、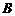 、
、 、
、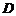 ,投掷时正面向上的概率如下表所示
,投掷时正面向上的概率如下表所示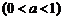 .
.
|
纪念币 |
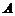 |
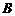 |
 |
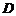 |
|
概率 |
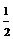 |
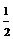 |
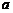 |
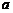 |
这四个纪念币同时投掷一次,设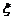 表示出现正面向上的个数.
表示出现正面向上的个数.
(Ⅰ)求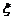 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在概率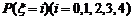 中,若
中,若 的值最大,求
的值最大,求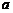 的取值范围;
的取值范围;
(文)(本大题满分12分)
一项体育比赛按两轮排定名次,每轮由A、B两种难度系数的4个动作构成。某选手参赛方案如表所示:
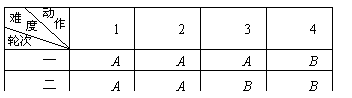

若这个选手一次正确完成难度系数为A、B动作的概率分别为0.8和0.5
(Ⅰ)求这个选手在第一轮中恰有3个动作正确完成的概率;
(Ⅱ)求这个选手在第二轮中两种难度系数的动作各至少正确完成一个概率。
17、(本大题满分12分)
已知函数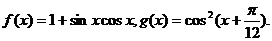
(Ⅰ)设 图象的一条对称轴,求
图象的一条对称轴,求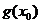 的值;
的值;
(Ⅱ)求使函数 上
上
是增函数的 的最大值.
的最大值.
16、平面 、
、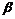 、
、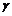 两两互相垂直,点
两两互相垂直,点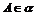 ,点A到
,点A到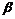 、
、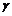 的距离都是3,P是
的距离都是3,P是 上的动点,P到
上的动点,P到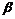 的距离是到点A距离的2倍,则点P的轨迹上的点到
的距离是到点A距离的2倍,则点P的轨迹上的点到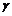 的距离的最小值是__________
的距离的最小值是__________
15、(理)已知抛物线 (p为常数,
(p为常数, )上不同两点A、B的横坐标恰好是关于x的方程
)上不同两点A、B的横坐标恰好是关于x的方程 (q为常数)的两个根,则直线AB的方程为
.
(q为常数)的两个根,则直线AB的方程为
.
(文)已知抛物线 (p为常数,
(p为常数, )上不同两点A、B的横坐标恰好是关于x的方程
)上不同两点A、B的横坐标恰好是关于x的方程 的两个根,则直线AB的方程为__________________
的两个根,则直线AB的方程为__________________
14、(理)设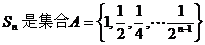 的所有3元子集的元素和之和,则
的所有3元子集的元素和之和,则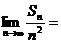 .
.
(文)设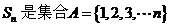 的所有3元子集的元素和之和,则
的所有3元子集的元素和之和,则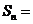
13、
在△ABC中,若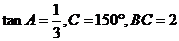 ,则AB=
.
,则AB=
.
12、已知函数 是定义在
是定义在 上的偶函数,且对任意
上的偶函数,且对任意 ,都有
,都有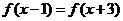 。当
。当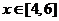 时,
时,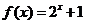 ,设函数
,设函数 在区间
在区间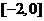 上的反函数为
上的反函数为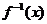 ,则
,则 的值为
的值为
A. B.
B.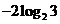 C.
C.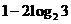 D.
D.
第Ⅱ卷(共90分)
11、(理)正方体ABCD-A1B1C1D1的各个顶点与各棱的中点共20个点中,任取两点连成直线,在这些直线中任取一条,它与BD1 垂直的概率为
A. 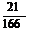 B.
B. C.
C.  D.
D.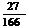
(文)正方体ABCD-A1B1C1D1的各个顶点与各棱的中点共20个点中,任取两点连成直线,与BD1 垂直的直线条数为
A.18 B.21 C. 27 D.12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com