
3.默写古诗文名句,并写出相应的作家、篇名。(10分)
①学而时习之,不亦说乎? ,不亦乐乎?(《<论语>八则》)
② ,长河落日圆。( 《使至塞上》)
③感时花溅泪, 。(杜甫《春望》)
④ ,却话巴山夜雨时。(李商隐《 》)
⑤ ,月如钩。寂寞梧桐深院锁清秋。(李煜《相见欢》)
⑥落红不是无情物, 。(龚自珍《己亥杂诗》)
⑦予独爱莲之 ,濯清涟而不妖……(周敦颐《爱莲说》)
⑧而或长烟一空,皓月千里, , ……(范仲淹《岳阳楼记》)
10.某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点,如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
解:将8个职工每一种下车的情况作为1个基本事件,那么共有38=6561(个)基本事件.
(1)记“该车在某停车点停车”为事件A,事件A发生说明在这个停车点有人下车,即至少有一人下车,这个事件包含的基本事件较复杂,于是我们考虑它的对立事件 ,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
∵P( )=
)=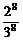 =
=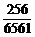 ,
,
∴P(A)=1-P( )=1-
)=1-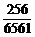 =
=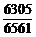 .
.
(2)记“停车的次数不少于2次”为事件B,则“停车次数恰好1次”为事件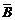 ,则P(B)=1-P(
,则P(B)=1-P(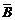 )=1-
)=1-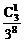 =1-
=1-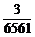 =
=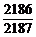 .
.
(3)记“恰好停车2次”为事件C,事件C发生就是8名职工在其中2个停车点下车,每个停车点至少有1人下车,所以该事件包含的基本事件数为C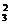 (C
(C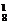 +C
+C +C
+C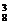 +…+C
+…+C )=3×(28-2)=3×254,于是P(C)=
)=3×(28-2)=3×254,于是P(C)=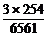 =
=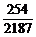 .
.
[探索题]袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为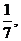 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用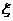 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中原有的白球的个数;(II)求取球两次终止的概率;(III)求甲取到白球的概率.
解:(I)设袋中原有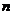 个白球,由题意知
个白球,由题意知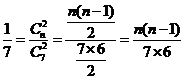
可得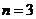 或
或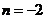 (舍去),即袋中原有3个白球。
(舍去),即袋中原有3个白球。
(II)记“取球两次终止” 的事件为 ,则
,则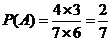 。
。
(III) 记“甲取到白球”的事件为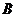 ,“第
,“第 次取出的球是白球”的事件为
次取出的球是白球”的事件为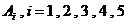 。
。
因为甲先取,所以甲只有可能在第1次,第3次取球和第5次取球,
∴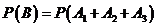 。因为事件
。因为事件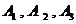 两两互斥,
两两互斥,
∴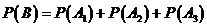
=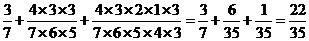
9.袋中有红、黄、白色球各一个,每次任取一个,有放回抽三次,计算下列事件的概率:
(1)三次颜色各不同;(2)三种颜色不全相同;(3)三次取出的球无红色或无黄色;
解:基本事件有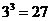 个,是等可能的,
个,是等可能的,
(1)记“三次颜色各不相同”为 ,
,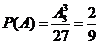 ;
;
(2)记“三种颜色不全相同”为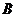 ,
,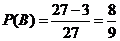 ;
;
(3)记“三次取出的球无红色或无黄色”为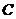 ,
,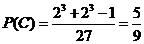 ;
;
8.某单位36人的血型类型是:A型12人,B型10人,AB型8人,O型6人.现从这36人中任选2人.
求:(1)两人同为A型血的概率;
(2)两人具有不相同血型的概率.
解:(1)P=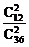 =
=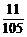 .
.
(2)考虑对立事件:两人同血型为事件A,
那么P(A)=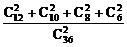 =
=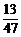 .
.
所以不同血型的概率为P=1-P(A)=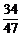 .
.
7. 9个国家乒乓球队中有3个亚洲国家队,抽签分成甲、乙、丙三组(每组3队)进行预赛,试求:
(1)三个组各有一个亚洲队的概率;
(2)至少有两个亚洲队分在同一组的概率.
解:9个队分成甲、乙、丙三组有C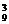 C
C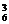 C
C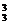 种等可能的结果.(1)三个亚洲国家队分给甲、乙、丙三组,每组一个队有A
种等可能的结果.(1)三个亚洲国家队分给甲、乙、丙三组,每组一个队有A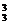 种分法,其余6个队平分给甲、乙、丙三组有C
种分法,其余6个队平分给甲、乙、丙三组有C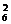 C
C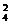 C
C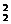 种分法.故三个组各有一个亚洲国家队的结果有A
种分法.故三个组各有一个亚洲国家队的结果有A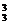 ·C
·C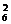 C
C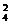 C
C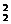 种,所求概率
种,所求概率
P(A)=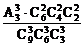 =
=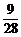 .
.
答:三个组各有一个亚洲国家队的概率是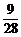 .
.
(2)∵事件“至少有两个亚洲国家队分在同一组”是事件“三个组各有一个亚洲国家队”的对立事件,∴所求概率为1-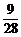 =
=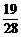 .
.
答:至少有两个亚洲国家队分在同一组的概率是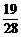 .
.
6.法一:所有分组方法有: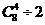 种,两强队在一组的分法有:
种,两强队在一组的分法有: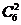 种,故所求概率为P=
种,故所求概率为P=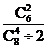 =
=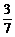 . 法二:P=1-
. 法二:P=1-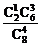 =1-
=1-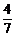 =
=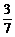 .
.
[解答题]
5.分2张和3张相同:P=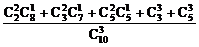 =
=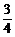 .
.
6.将8个队分成两个组,每组4个队进行比赛,其中这两个强队被分在一个组内的概率是________.
◆练习简答:1.C; 2. P=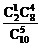 +
+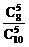 =
=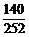 +
+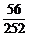 =
= ; 3.分先摸白球和黑球两种情况: P=
; 3.分先摸白球和黑球两种情况: P=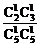 +
+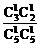 =
=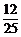 ; 4. P=1-
; 4. P=1-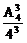 =
=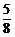 ;
;
5.有10张人民币,其中伍元的有2张,贰元的有3张,壹元的有5张,从中任取3张,则3张中至少有2张的币值相同的概率为________.
4.有3人,每人都以相同的概率被分配到4个房间中的一间,则至少有2人分配到同一房间的概率是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com