
7.在△ABC中, =a,
=a, =b,M是CB的中点,N是AB的中点,且CN、AM交于点P,则
=b,M是CB的中点,N是AB的中点,且CN、AM交于点P,则 可用a、b表示为
.
可用a、b表示为
.
答案 - a+
a+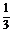 b
b
6.已知平面内有一点P及一个△ABC,若 +
+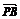 +
+ =
= ,则点P在线段
上.
,则点P在线段
上.
答案 AC
5.设 =x
=x +y
+y ,且A、B、C三点共线(该直线不过端点O),则x+y=
.
,且A、B、C三点共线(该直线不过端点O),则x+y=
.
答案 1
4. 如图所示,平面内的两条相交直线OP1和OP2将该平面
如图所示,平面内的两条相交直线OP1和OP2将该平面
分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若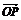
=a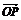 1+b
1+b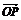 2,且点P落在第Ⅲ部分,则实数a,b满足
2,且点P落在第Ⅲ部分,则实数a,b满足
a 0,b 0.(用“>”,“<”或“=”填空)
答案 > <
3.若 =3e1,
=3e1, =-5e1,且|
=-5e1,且| |=|
|=| |,则四边形ABCD是
.
|,则四边形ABCD是
.
答案 等腰梯形
2.(2008·全国Ⅰ理)在△ABC中, =c,
=c, =b,若点D满足
=b,若点D满足 =2
=2 ,则
,则 = (用b,c表示).
= (用b,c表示).
答案  b+
b+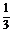 c
c
1.下列算式中正确的是 (填序号).
① +
+ +
+ =0 ②
=0 ② -
- =
= ③0·
③0· =0 ④
=0 ④ (
(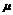 a)=
a)= ·
·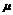 ·a
·a
答案 ①③④
20. (2008·浙江理,18) (16分)如图所示,矩形ABCD和梯形BEFC所在平面互相垂直,
(2008·浙江理,18) (16分)如图所示,矩形ABCD和梯形BEFC所在平面互相垂直,
BE∥CF,∠BCF=∠CEF=90°,AD= ,EF=2.
,EF=2.
(1)求证:AE∥平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为60°?
方法一 (1)证明 过点E作EG⊥CF交CF于G,
连接DG.可得四边形BCGE为矩形,
又四边形ABCD为矩形,
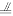 所以AD EG,从而四边形ADGE为平行四边形,
所以AD EG,从而四边形ADGE为平行四边形,
故AE∥DG.
因为AE 平面DCF,DG
平面DCF,DG 平面DCF,
平面DCF,
所以AE∥平面DCF.
 (2)解 过点B作BH⊥EF交FE的延长线于H,连接AH.
(2)解 过点B作BH⊥EF交FE的延长线于H,连接AH.
由平面ABCD⊥平面BEFC,AB⊥BC,
得AB⊥平面BEFC,
从而AH⊥EF,所以∠AHB为二面角A-EF-C的平面角.
在Rt△EFG中,因为EG=AD= ,EF=2,
,EF=2,
所以∠CFE=60°,FG=1,
又因为CE⊥EF,所以CF=4,
从而BE=CG=3.
于是BH=BE·sin∠BEH=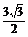 .
.
因为AB=BH·tan∠AHB=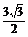 ×
× =
= ,
,
所以当AB为 时,二面角A-EF-C的大小为60°.
时,二面角A-EF-C的大小为60°.
方法二 如图所示,以点C为坐标原点,以CB、CF和CD所在直线分别作为x轴、y轴和z轴,建立空间直角坐标系C-xyz.

设AB=a,BE=b,CF=c,
则C(0,0,0),A( ,0,a),
,0,a),
B( ,0,0),E(
,0,0),E( ,b,0),F(0,c,0).
,b,0),F(0,c,0).
(1)证明 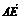 =(0,b,-a),
=(0,b,-a), =(
=( ,0,0),
,0,0),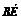 =(0,b,0),
=(0,b,0),
所以 ·
·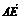 =0,
=0, ·
· =0,从而CB⊥AE,CB⊥BE.
=0,从而CB⊥AE,CB⊥BE.
AE∩BE=E,所以CB⊥平面ABE.
因为CB⊥平面DCF,
所以平面ABE∥平面DCF,AE 平面ABE.
平面ABE.
故AE∥平面DCF.
(2)解 因为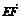 =(-
=(- ,c-b,0),
,c-b,0), =(
=( ,b,0).
,b,0).
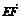 ·
· =0,|
=0,|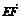 |=2,
|=2,
所以 解得
解得
所以E( ,3,0),F(0,4,0).
,3,0),F(0,4,0).
设n=(1,y,z)与平面AEF垂直,
则n·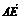 =0,n·
=0,n·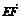 =0,解得n=(1,
=0,解得n=(1, ,
, ).
).
又因为BA⊥平面BEFC, =(0,0,a),
=(0,0,a),
所以|cos〈n,  〉|=
〉|=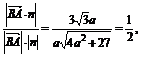
解得a= .
.
所以当AB为 时,二面角A-EF-C的大小为60°.
时,二面角A-EF-C的大小为60°.
19.(16分)如图所示,在矩形ABCD中,AB=2BC=2a,E为AB上一点,将B点沿线段EC折起至点P,连接PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
 (1)试确定E点位置;
(1)试确定E点位置;
(2)若异面直线PE、CD所成的角为60°,并且PA的长度大于a,
求证:平面PEC⊥平面AECD.
(1)解 E为AB的中点.
证明如下:取PC的中点G,连接GE,GF.
 由条件知GF∥CD,EA∥CD,∴GF∥EA.
由条件知GF∥CD,EA∥CD,∴GF∥EA.
则G、E、A、F四点共面.
∵AF∥平面PEC,
平面GEAF∩平面PEC=GE,
∴FA∥GE.
则四边形GEAF为平行四边形.
∴GF=AE,∵GF=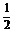 CD,∴EA=
CD,∴EA=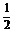 CD=
CD=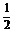 BA.
BA.
即E为AB的中点.
(2)证明 ∵EA∥CD,PE、CD所成的角为60°,且PA的长度大于a.
∴∠PEA=120°.
∵PE=BE=EA=a,∴PA= a.
a.
取CE的中点M,连接PM,AM,BM,在△AEM中,
AM=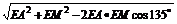 =
= a.
a.
∵PM=BM=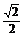 a,∴PM2+AM2=PA2.
a,∴PM2+AM2=PA2.
则∠PMA=90°,PM⊥AM.
∵PM⊥EC,EC∩AM=M,
∴PM⊥平面AECD.
∵PM 平面PEC,
平面PEC,
∴平面PEC⊥平面AECD.
18. (16分)三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,
(16分)三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,
∠BAC=90°,A1A⊥平面ABC,A1A= ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
=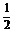 .
.
(1)证明:平面A1AD⊥平面BCC1B1;
(2)求二面角A-CC1-B的余弦值.
方法一 (1)证明 ∵A1A⊥平面ABC,BC 平面ABC,
平面ABC,
∴A1A⊥BC.
在Rt△ABC中,AB= ,AC=2,∴BC=
,AC=2,∴BC=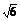 .
.
∵BD∶DC=1∶2,∴BD= .又
.又 =
= =
= ,
,
∴△DBA∽△ABC,∴∠ADB=∠BAC=90°,
即AD⊥BC.
又A1A∩AD=A,∴BC⊥平面A1AD.
∵BC 平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
平面BCC1B1,∴平面A1AD⊥平面BCC1B1.
 (2)解 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1,
(2)解 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1,
∴AE是BE在平面ACC1A1内的射影.
由三垂线定理知BE⊥CC1,
∴∠AEB为二面角A-CC1-B的平面角. 图①
过C1作C1F⊥AC交AC于F点,
则CF=AC-AF=1,
C1F=A1A= ,∴∠C1CF=60°.
,∴∠C1CF=60°.
在Rt△AEC中,
AE=ACsin60°=2× =
= ,
,
在Rt△BAE中,tan∠AEB= =
= =
= ,
,
∴cos∠AEB= ,
,
即二面角A-CC1-B余弦值为 .
.
方法二 (1) 证明 如图②,建立空间直角坐标系,
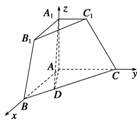
图②
则A(0,0,0),B( ,0,0),C(0,2,0),
,0,0),C(0,2,0),
A1(0,0, ),C1(0,1,
),C1(0,1,  ).
).
∵BD∶DC=1∶2,∴ =
=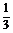
 ,
,
∴D点坐标为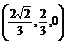 ,
,
∴ =
=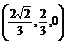 ,
, =(-
=(- ,2,0),
,2,0), =(0,0,
=(0,0, ).
).
∵ ·
· =0,
=0, ·
· =0,
=0,
∴BC⊥AA1,BC⊥AD.又A1A∩AD=A,
∴BC⊥平面A1AD.又BC 平面BCC1B1,
平面BCC1B1,
∴平面A1AD⊥平面BCC1B1.
(2)解 ∵BA⊥平面ACC1A1,取m= =(
=( ,0,0)为平面ACC1A1的法向量.
,0,0)为平面ACC1A1的法向量.
设平面BCC1B1的法向量为n=(x,y,z),
则 ·n=0,
·n=0, ·n=0,
·n=0,
∴
∴x= y,z=
y,z=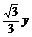 ,可取y=1,则n=
,可取y=1,则n= ,
,
cos〈m,n〉=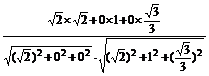
= ,
,
即二面角A-CC1-B的余弦值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com