
4、如果两个平行平面同时和第三个平面相交,那么它们的交线平行
3、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行
2、垂直于同一平面的两条直线互相平行
1、平行于同一直线的两条直线互相平行
4. (1997年全国高考)如图,在正方体
(1997年全国高考)如图,在正方体 中,E,F分别是
中,E,F分别是 的中点.
的中点.
Ⅰ.证明AD⊥ ;
;
Ⅱ.求AE与 所成的角;
所成的角;
Ⅲ.证明面AED⊥面 ;
;
Ⅳ.设 =2,求三棱锥
=2,求三棱锥 的体积
的体积
[答案与提示: (2)90º; (4) =1]
=1]
3.(2002年北京高考)如图:在多面体 中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E、F两点,上下底面矩形的长、宽分别为
中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E、F两点,上下底面矩形的长、宽分别为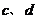 与
与 ,且
,且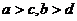 ,两底面间的距离为
,两底面间的距离为 。
。
(1)求侧面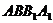 与底面
与底面 所成二面角的大小;
所成二面角的大小;
 (2)证明:
(2)证明:
(3)在估测该多面体的体积时,经常运用近似公式 来计算。已知它的体积公式是
来计算。已知它的体积公式是 。
。
试判断 与
与 的大小关系,并加以证明。
的大小关系,并加以证明。
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面)
答案与提示:(1)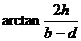 ;(3)
;(3) 。
。
2.(2002年全国高考)如图:正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动,点N在BF上移动,若CM=BN=
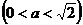 .
.
(Ⅰ)求MN的长;
(Ⅱ)当 为何值时,MN的长最小;
为何值时,MN的长最小;
(Ⅲ)当MN的长最小时,求面MNA与面MNB所成的二面角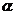 的大小。
的大小。
[答案与提示:(Ⅰ)
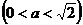 ;(Ⅱ)
;(Ⅱ) 时,MN的长最小,为
时,MN的长最小,为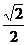 ;(Ⅲ)
;(Ⅲ) ]
]
1.(2000年全国高考题)如图,已知平行六面体ABCD- 的底面ABCD是菱形,且
的底面ABCD是菱形,且 =
= =
=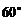 。
。
 (I)证明:
(I)证明: ⊥BD;
⊥BD;
(II)假定CD=2, =
= ,记面
,记面 为
为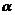 ,面CBD为
,面CBD为 ,求二面角
,求二面角  的平面角的余弦值;
的平面角的余弦值;
(III)当 的值为多少时,能使
的值为多少时,能使 平面
平面 ?请给出证明。
?请给出证明。
 [答案与提示:(Ⅰ)略;(Ⅱ)
[答案与提示:(Ⅰ)略;(Ⅱ) ;(Ⅲ)
;(Ⅲ) =1。
=1。
6.如图,正方体的棱长为1, ,求:(1)
,求:(1)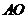 与
与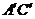 所成角;
所成角;
(2)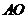 与平面
与平面 所成角的正切值;(3)平面
所成角的正切值;(3)平面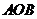 与平面
与平面 所成角
所成角
7 ?已知正方体
?已知正方体 的棱长为
的棱长为 ,
, 是
是 的中点,
的中点,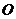 是对角线
是对角线 的中点,
的中点,
(1)求证: 是异面直线
是异面直线 和
和 的公垂线;(2)求异面直线
的公垂线;(2)求异面直线 和
和 的距离
的距离
5.如果二面角 的平面角是锐角,点
的平面角是锐角,点 到
到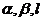 的距离分别为
的距离分别为 ,求二面角的大小
,求二面角的大小
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com