1.(2005广东)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6)，骰子朝上的面的点数分别为X、Y，则的概率为　　 ( 　)

A．　　　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　 D．

6.求概率的方法:

(1)等可能性事件的概率,步骤:

①明确事件A的意义,确定是否等可能性事件.

②求出一次实验可能出现的结果的总数n;

求m,n时,要注意是否与顺序、位置有关，是“有放回”还是“无放回”抽取，正确排列、组合公式或计数原理求出分母n和分子m;(分子、分母可以与顺序同时有关或无关，解题时可以灵活处理)。

③用等可能性事件概率公式P=求出概率值.

(2)通过进行大量的重复试验，用这个事件发生的频率近似地作为它的概率.

5.等可能性事件的概率：在等可能事件中,如果事件包含个结果，那么事件的概率.

4.等可能性事件：如果一次试验中有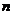个可能的结果--称为基本事件，且每个基本事件出现的可能性都相等，即每个基本事件的概率都是，这种事件叫等可能性事件.

3.概率的性质：(由定义知,0≤m≤1,) ∴ ;

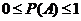必然事件的概率为,不可能事件的概率为.

必然事件和不可能事件看作随机事件的两个极端情形.

2.随机事件的概率：一般地，在大量重复进行同一试验时，事件A发生的频率总是接近某个常数，在它附近摆动，这时就把这个常数叫做事件A的概率，记作P(A).

1.事件的定义：

随机事件：在一定条件下可能发生也可能不发生的事件；

必然事件：在一定条件下必然发生的事件；

不可能事件：在一定条件下不可能发生的事件.

2.了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率.

1.了解随机事件的发生存在着规律性和随机事件概率的意义;

2、　　 如图，运动会上一名服务的同学要往返于百米起跑点A、终点记时处B(A、B位于东西方向)及检录处C，他在A处看C点位于北偏东60°方向上，在B处看C点位于西北方向(即北偏西45°)上。

(1)确定检录处C的位置；

(2)现限定只用刻度尺作为工具，如果想知道这位同学在检录处C与百米起跑点A之间往返一次要走多少米(不考虑其他因素)，你有什么办法？(要求：只写出一种办法，不需具体计算)

解：