
11、若一个数的平方是正数,则它是负数 12、 170 、 171.5
16、袋中有大小、形状相同的红、黑球各一个,现依次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
基础训练02、
一 选择题
二 填空题
破釜沉舟!!攻克语音关!(22)
|
400 |
痉挛 |
|
410 |
羞赧 |
|
|
401 |
皱缬 |
|
411 |
耄耋 |
|
|
402 |
监生 |
|
412 |
胳臂 |
|
|
403 |
砥柱 |
|
413 |
胼胝 |
|
|
404 |
秘鲁 |
|
414 |
脊梁 |
|
|
405 |
租赁 |
|
415 |
脑髓 |
|
|
406 |
窈窕 |
|
416 |
荷枪 |
|
|
407 |
笑靥 |
|
417 |
荷蓧 |
|
|
408 |
绦虫 |
|
418 |
莅临 |
|
|
409 |
罢黜 |
|
419 |
莞尔 |
|
6.下面是近期网络上的一则新闻,有多处错误,或标点不当,或有语病,或不连贯。请找出四处并加以修改。(4分)
12月1日是世界艾滋病日,今年的宣传主题是“遏制艾滋、履行承诺”①。目前,艾滋病在中国逐步流行并呈现快速上升趋势②,已经从高危人群向一般人群③。
科学研究事实证明④,在工作和生活中与艾滋病感染者和病人的一般接触⑤,如握手、拥抱、礼节性接吻、共进晚餐、共用劳动工具、办公用品、钱币等不会感染艾滋病⑥。
艾滋病不会经马桶圈、电话机、餐饮机、卧具、游泳池、公共设施传播⑦。咳嗽、打喷嚏以及蚊虫不传播艾滋病⑧。
序号 改正
序号 改正
序号 改正
序号 改正
5.请仿照下面广州某校为“迎2010广州亚运会”活动拟写的标语形式,为2007年“菏泽国际牡丹花会”拟写一则宣传标语。要求:主题突出,内容相关,结构大致相同。(4分)
广州亚运会:珠水欢腾,喜迎亚洲健儿
菏泽国际牡丹花会:
4.下列句子衔接合理且语言典雅工整的一项是( )
A. 没有到过昆明的人,总以为这地方四季皆好,在这里住久的人,却以为冬天最美。_______________________________
A. 冬天无风无雨,天空最高最蓝,花色最多最妍,五百里滇池,净水明山,山上无云霭;数峰青碧。
B.天空最高最蓝,冬天无风无雨,花色最多最妍,五百里滇池,净水明山,山上无云霭,数峰青碧。
C. 冬天无风无雨,天空最高最蓝,花色最多最妍,滇池五百里,水净山明,山上无云霭,数峰青碧。
D. 天空最高最蓝,冬天无风无雨,花色最多最妍,滇池五百里,水净山明,山上无云霭,数峰青碧。
3.下列各句中,没有语病的一句是( )
A.由于三鹿牌婴幼儿奶粉的三聚氰胺含量严重超标,导致不少婴幼儿患上结石病,在社会上造成了极坏的影响。
B.奥运会结束后,国家体育场“鸟巢”和“水立方”的清场工作基本完成,将在两个星期之后迎来第一批游客。
C. 有专家认为,以标榜草根创新精神为幌子的山寨文化泛滥的原因,是由于中国知识产权意识严重缺位所致。
D. 国家允许农民以砖包、出租、互换、转让、股份合作等形式流转土地承包经营权,发展多种形式的适度规模经营。
2.下列各句中,加点的成语使用恰当的一句是( )
A.由美国次贷危机引发的金融风暴,以风卷残云之势在两周内迅速蔓延到世界各地,其影
响之大让人始料不及。
B.2008年5月12日四川汶川等地区发生了里氏8.0级强烈地震,破环十分严重,整个汶川县城更是千疮百孔。
C.在北京第29届奥运会三米跳板比赛中,名将郭晶晶最后一跳尽善尽美,接近满分,最终获得该项目冠军。
D.随着政府加大对教育的投人,一些农村学校的师资力量和教学设备已经可以和城市学校
同日而语了。
(安徽省合肥市2008/2009学年度高三期末调研考试)
1.下列词语中加点的字,每对读音都不相同的-组是( )
A. 处境/处理 裨将/大有裨益 擂台/擂鼓助威
B.累赘/累积 慰藉/杯盘狼藉 估量/量体裁衣
C.干劲/遒劲 横竖/满脸横肉 角力/勾心斗角
D. 创伤/重创 奢靡/所向披靡 押解/浑身解数

B、C、D,应选A.
[说明] 此例题用多种方法求解选项,指出3种选择题的技巧.




∴应选D

x轴交点中在原点右边最接近原点的交点,而在原点左边与x轴交点中最


的图象.
∴选D
[说明] y=Asin(ωx+j)(A>0,ω>0)x∈R的图象可由y=sinx的图象经下列各种顺序变换得到的.
(1)先平移,后伸缩:
①把y=sinx的图象向左(j>0)或向右(j<0)沿x轴方向平移|j|个单位;(相位变换)

(周期变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍,横坐标不变(振幅变换)
(2)先伸缩,后平移
①把y=sinx图象上各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原


(相位变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍横坐标不变(振幅变换)

再把横坐标缩小到原来的一半,纵坐标扩大到原来的4倍,则所得的图象的解析式是 [ ]



∴选A.
[例17] 方程sin2x=sinx在区间(0,2π)内解的个数是
[ ]
A.1 B.2 C.3 D.4
[分析] 本题有两类解法
(1)求出方程在(0,2π)内的所有解,再数其解的个数.而决定选项,对于选择题,此法一般不用.
(2)在同一坐标系中作出函数y=sin2x和y=sinx的图象,如图2-18所示.

它们在(0,2π)内交点个数,即为所求方程解的个数,从而应选C.
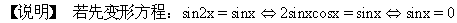

它体现了数、形的结合.
[例18] 设函数f(x)是定义在R上的周期为3的奇函数,且f(1)=2,则f(5)=____
解:∵f(x)是奇函数,且f(1)=2,∴f(-1)=-2
又∵f(x)是周期为3的函数. ∴f(3+x)=f(x)
∴f(-1+3)=f(-1)=-2 即f(2)=-2
f(2+3)=f(2)=-2 即f(5)=-2
[例19] 有一块扇形铁板,半径为R,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都在扇形的半径或弧上,求这个内接矩形的最大面积.
[分析] 本题入手要解决好两个问题.
(1)内接矩形的放置有两种情况,如图2-19所示,应该分别予以处理.
(2)求最大值问题这里应构造函数,怎么选择便于以此表达矩形面积的自变量.

解:如图2-19(1)设∠FOA=θ,则FG=Rsinθ
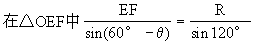
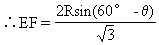
又设矩形EFGH的面积为S,那么
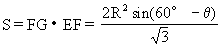

又∵0°<θ<60°,故当cos(2θ-60°)=1,即θ=30′时,

如图2-19 (2),设∠FOA=θ,则EF=2Rsin(30°-θ),在△OFG中,∠OGF=150°

设矩形的面积为S.
那么S=EFFG=4R2sinθsin(30°-θ)
=2R2[cos(2θ-30°)-cos30°]
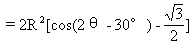
又∵0<θ<30°,故当cos(2θ-30°)=1


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com