
本部分考试大纲要求如下:
(1)函数
① 了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.
② 在实际情境中,会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数.
③ 了解简单的分段函数,并能简单应用.
④ 理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解函数奇偶性的含义.
⑤ 会运用函数图像理解和研究函数的性质.
(2)指数函数
① 了解指数函数模型的实际背景.
② 理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
③ 理解指数函数的概念,并理解指数函数的单调性掌握指数函数图像通过的特殊点.
④ 知道指数函数是一类重要的函数模型.
(3)对数函数
① 理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
② 理解对数函数的概念;理解对数函数的单调性,掌握函数图像通过的特殊点.
③ 知道对数函数是一类重要的函数模型;
④ 了解指数函数 与对数函数
与对数函数 互为反函数(
互为反函数(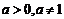 ).
).
(4)幂函数
① 了解幂函数的概念.
② 结合函数 的图像,了解它们的变化情况.
的图像,了解它们的变化情况.
(5)函数与方程
① 结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.
② 根据具体函数的图像,能够用二分法求相应方程的近似解.
(6)函数模型及其应用
① 了解指数函数、对数函数以及幂函数的增长特征.知道直线上升、指数增长、对数增长等不同函数类型增长的含义.
② 了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
22.(陕西师大附中2008年高三第八次)(Ⅰ)已知函数 ,求证:函数
,求证:函数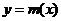 在区间
在区间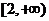 上为减函数;
上为减函数;
(Ⅱ)已知函数 ,若在
,若在 上至少存在一点
上至少存在一点 , 使得
, 使得 成立,求实数
成立,求实数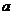 的取值范围.
的取值范围.
21.解关于 的不等式:
的不等式:
20.已知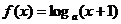 ,点P是函数y=f(x)图象上任意一点,点P关于原点的对称点Q的轨迹是函数y=g(x)的图象.
,点P是函数y=f(x)图象上任意一点,点P关于原点的对称点Q的轨迹是函数y=g(x)的图象.
(1)当0<a<1时,解不等式:2f(x)+g(x)≥0;
(2)当a>1,x∈ 时,总有2f(x)+g(x)≥m恒成立,求m的范围.
时,总有2f(x)+g(x)≥m恒成立,求m的范围.
19.设f(x)是定义在 的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当
的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当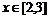 时,
时, .(1)求f(x)的解析式;(2)对于任意的
.(1)求f(x)的解析式;(2)对于任意的 求证:
求证: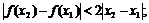 (3)对于任意的
(3)对于任意的 求证:
求证: (14分)
(14分)
18、(浙江省重点中学2008年5月)已知函数 ,数列
,数列 的前
的前 项和为
项和为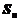 ,
, ,且
,且
 .(Ⅰ)求
.(Ⅰ)求 的最大值;(Ⅱ)证明:
的最大值;(Ⅱ)证明: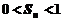 ;(Ⅲ)探究:数列
;(Ⅲ)探究:数列 是否单调?
是否单调?
17、已知函数 的图象与
的图象与 轴分别相交于点A、B,
轴分别相交于点A、B, (
( 分别是与
分别是与 轴正半轴同方向的单位向量),函数
轴正半轴同方向的单位向量),函数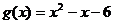 .
.
(1)求 的值;(2)当
的值;(2)当 满足
满足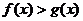 时,求函数
时,求函数 的最小值.
的最小值.
16、设a,b ÎR+,且a+b =1,则 的最大值是_____.
的最大值是_____.
15、已知点(x0,y0)在直线ax+by=0,(a,b为常数)上,则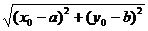 的最小值为 .
的最小值为 .
14.若a,b,c>0且a(a+b+c)+bc=4-2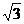 ,则2a+b+c的最小值为
,则2a+b+c的最小值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com