
5.双曲线的标准方程及其几何性质:
|
标准方程 |
 |
 |
|
图形 |
 |
 |
|
顶点 |
 |
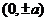 |
|
对称轴 |
 轴, 轴, 轴,实轴长为 轴,实轴长为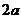 ,虚轴长为 ,虚轴长为 |
|
|
焦点 |
 |
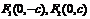 |
|
焦距 |
焦距为  |
|
|
离心率 |
  (e>1) (e>1) |
|
|
准线方程 |
 |
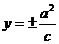 |
4.双曲线的定义:
第一定义:平面内到两个定点F1、F2的距离之差的绝对值等于定值2a(0<2a<|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.
第二定义: 平面内到定点F与到定直线l的距离之比是常数e(e>1)的点的轨迹是双曲线,定点叫做双曲线的焦点,定直线 叫做双曲线的准线,常数
叫做双曲线的准线,常数 叫做双曲线的离心率.
叫做双曲线的离心率.
3.椭圆知识网络

2.椭圆的标准方程及其几何性质:
|
标准方程 |
 |
 |
|
图形 |
 |
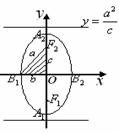 |
|
顶点 |
 , , |
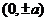 , , |
|
对称轴 |
 轴, 轴, 轴,长轴长为 轴,长轴长为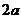 ,短轴长为 ,短轴长为 |
|
|
焦点 |
 、 、 |
 、 、 |
|
焦距 |
焦距为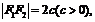  |
|
|
离心率 |
 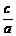 (0<e<1) (0<e<1) |
|
|
准线方程 |
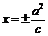 |
 |
1.椭圆的定义:
第一定义:平面内到两个定点F1、F2的距离之和等于定值2a(2a>|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.
第二定义: 平面内到定点F与到定直线l的距离之比是常数e(0<e<1)的点的轨迹是椭圆,定点叫做椭圆的焦点,定直线 叫做椭圆的准线,常数
叫做椭圆的准线,常数 叫做椭圆的离心率.
叫做椭圆的离心率.
(二)考点预测题
1.(2008年山东卷,数学理科,4)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值为
(A) 3 (B)2 (C)1 (D)-1
[解析]本题考查函数的性质,函数的性质是重点考查内容,对函数的几个性质应熟练掌握,09高考必将有涉及函数性质的题目出现, 、
、 在数轴上表示点
在数轴上表示点 到点
到点 、
、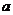 的距离,他们的和
的距离,他们的和 关于
关于 对称,因此点
对称,因此点 、
、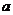 关于
关于 对称,所以
对称,所以 (直接去绝对值化成分段函数求解比较麻烦,如取特殊值解也可以)
(直接去绝对值化成分段函数求解比较麻烦,如取特殊值解也可以)
[答案]A
2.(2008年上海卷,数学文科,9)若函数 (常数
(常数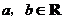 )是偶函数,且它的值域为
)是偶函数,且它的值域为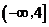 ,则该函数的解析式
,则该函数的解析式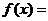 .
.
 [解析]本题考查函数的解析式,
[解析]本题考查函数的解析式, 是偶函数,则其图象关于y轴对称,
是偶函数,则其图象关于y轴对称, 
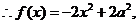 且值域为
且值域为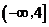 ,
, 

[答案]
3.(2008年广东卷,数学理科,19)设 ,函数
,函数 ,
,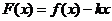 ,
,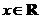 ,试讨论函数
,试讨论函数 的单调性.
的单调性.
[解析]本题考查函数的综合应用,广东连续两年均考查了函数解答题,江苏08年也以函数作为压轴题,应引起一定重视。
[答案]

对于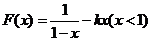 ,
,
当 时,函数
时,函数 在
在 上是增函数;
上是增函数;
当 时,函数
时,函数 在
在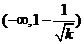 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
 对于
对于 ,
,
当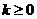 时,函数
时,函数 在
在 上是减函数;
上是减函数;
当 时,函数
时,函数 在
在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。

(一)文字介绍
本节内容在高考中占有一定比重,而且二分法是新增内容,应引起重视,同时对反函数的考查要求降低,本节多数题目将会以小题目出现,重点仍将是考查函数的性质,二分法,函数的定义域,以及函数的综合应用等知识点。
6. (山东省济宁市2009届高三11月教学质量检测,数学理科,20)函数
(山东省济宁市2009届高三11月教学质量检测,数学理科,20)函数 和
和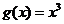 的图象的示意图如图4所示,设两函数的图象交于点
的图象的示意图如图4所示,设两函数的图象交于点 ,且
,且
(1)请指出示意图中 分别对应哪一个函数?
分别对应哪一个函数?
(2)若 ,
,
且 ,指出a,b的值,并说明理由;
,指出a,b的值,并说明理由;
(3)结合函数图象的示意图,判断
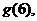
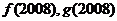 的大小,并按从小到大的顺序排列。
的大小,并按从小到大的顺序排列。
[解析]考查函数的综合运用
[答案](1) 对应的函数为
对应的函数为 ,
, 对应的函数为
对应的函数为
(2)
理由如下:
令 ,则
,则 为函数
为函数 的零点。
的零点。
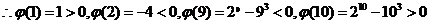 ,
,
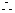 方程
方程 的两个零点
的两个零点
因此整数
(3)从图像上可以看出,当 时,
时,
当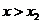 时,
时,

5.(安徽省六校2009年高三联考试卷,数学文科,11)己知 是偶函数,当
是偶函数,当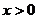 时,
时, ,且当
,且当 时
时 恒成立,则
恒成立,则 的最小值是( )
的最小值是( )
A  B
B  C 1
D
C 1
D 
[解析]本题考查函数的性质及函数在给定区间上的最值,当 时,
时, ,故
,故 恒成立,则
恒成立,则 的最小值是1
的最小值是1
[答案]C
4.(辽宁省沈阳二中2008-2009学年上学期高三期中考试,数学,8)定义在[-2,2]上的偶函数 时,
时,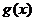 单调递减,若
单调递减,若 则实数m的取值范围是
。
则实数m的取值范围是
。
[解析]本题考查函数的性质,奇偶性,单调性的应用,由题意可知 故
故 解得
解得
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com