
2、计算 ⊙
⊙ 、
、 ⊙
⊙ 、
、 ⊙
⊙
 、
、
 ⊙
⊙
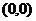 等……………………………………………………………………………1分
等……………………………………………………………………………1分
2.若 ,则
,则
所以
解得 ……………………………………………………………………………………..2分
……………………………………………………………………………………..2分
所以,存在 满足:对于任意
满足:对于任意 ,都有
,都有 ⊙
⊙
 ⊙
⊙ 成立………………..1分
成立………………..1分
(Ⅳ)1、举例计算,如计算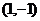 ⊙
⊙ 等不给分
等不给分
1.若 ,显然有
,显然有 ⊙
⊙ 成立;………………………………………………………1分
成立;………………………………………………………1分
2、(上海市闸北区09届高三数学(理)第18题)在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在 上定义一个运算,记为⊙,对于
上定义一个运算,记为⊙,对于 中的任意两个元素
中的任意两个元素
 ,规定:
,规定: ⊙
⊙
 .
.
(Ⅰ)计算: ⊙
⊙ ;
;
(Ⅱ)请用数学符号语言表述运算⊙满足交换律和结合律,并任选其一证明;
(Ⅲ) 中是否存在唯一确定的元素
中是否存在唯一确定的元素 满足:对于任意
满足:对于任意 ,都有
,都有 ⊙
⊙
 ⊙
⊙ 成立,若存在,请求出元素
成立,若存在,请求出元素 ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅳ)试延续对集合 的研究,请在
的研究,请在 上拓展性地提出一个真命题,并说明命题为真的理由.
上拓展性地提出一个真命题,并说明命题为真的理由.
答案:解:(Ⅰ) ⊙
⊙ ………………………………………………………….3分
………………………………………………………….3分
(Ⅱ)设 中的任意三个元素
中的任意三个元素
 ,
,
交换律: ⊙
⊙
 ⊙
⊙ ………………………………………………..4分
………………………………………………..4分
结合律:( ⊙
⊙ )⊙
)⊙
 ⊙(
⊙( ⊙
⊙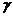 )
)
(Ⅲ)假设存在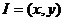 ,
, 则
则 ⊙
⊙ ,即
,即
 ⊙
⊙

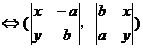
 …………………………………..2分
…………………………………..2分
1、(辽宁省抚顺一中2009届高三数学上学期第一次月考)
函数 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B.
的定义域为集合B.
(1)求A;
(2)若B A,求实数
A,求实数 的取值范围。
的取值范围。
答案:(1)A:x<-1或x≥1; --------------------------------4分
(2)B:(x-a-1)(x-2a)<0
∵φ≠B A,∴①
A,∴①
 ∴a>1
------------------------8分
∴a>1
------------------------8分
或② ∴a≤-2或
∴a≤-2或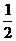 ≤a<1; ---------------------------11分
≤a<1; ---------------------------11分
∴a>1或a≤-2或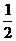 ≤a<1;
---------------------------------------12分
≤a<1;
---------------------------------------12分
4、(08江西文8)在△ABC中,设命题 命题q:△ABC是等边三角形,那么命题p是命题q的 ( )
命题q:△ABC是等边三角形,那么命题p是命题q的 ( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
答案:C.
评析:把解三角形与充分必要条件结合
考点四 综合性问题
3、(辽宁省抚顺一中2009届高三数学上学期第一次月考)
圆 与直线
与直线 有两个公共点的充要条件是( )
有两个公共点的充要条件是( )
A. B.
B.

C. 

 D.
D.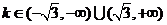
答案:D.
评析:把解析几何与充分必要条件结合
2、(上海市闸北区09届高三数学第11题)“函数 存在反函数”是“函数
存在反函数”是“函数 在
在 上为单调函数”的
( )
上为单调函数”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:B
评析:把函数单调性、反函数与充分必要条件结合
1、(07山东卷)设p:x -x-20>0,q:
-x-20>0,q: <0,则p是q的
<0,则p是q的
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
答案: p:x -x-20>0Ûx>5或x<-4,q:
-x-20>0Ûx>5或x<-4,q: <0Ûx<-2或-1<x<1或x>2,
<0Ûx<-2或-1<x<1或x>2,
 借助图形知选A
借助图形知选A
评析:把解不等式与充分必要条件结合
4、(07山东理7)
命题“对任意的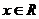 ,
, ”的否定是
”的否定是
(A)不存在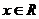 ,
, (B)存在
(B)存在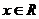 ,
,
(C)存在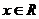 ,
, (D)对任意的
(D)对任意的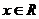 ,
,
答案:C
评析:注意两点:1)全称命题变为特称命题;2)只对结论进行否定。
考点三 充分必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com