2. 平衡条件

　　 共点力作用下物体的平衡条件是所受合外力为零，即。

1. 平衡状态

　　 指的是静止或匀速直线运动状态。特点：。

2. 公式：

　　 理解要点：

　　 ①因果性：是产生加速度a的原因，它们同时产生，同时变化，同时存在，同时消失；

　　 ②方向性：a与都是矢量，方向严格相同；

　　 ③瞬时性和对应性：a为某时刻某物体的加速度，是该时刻作用在该物体上的合外力。

1. 定律内容

　　 物体的加速度a跟物体所受的合外力成正比，跟物体的质量m成反比。

　　 一切物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止。

　　 (1)理解要点：

　　 ①运动是物体的一种属性，物体的运动不需要力来维持。

　　 ②它定性地揭示了运动与力的关系：力是改变物体运动状态的原因，是使物体产生加速度的原因。

　　 ③第一定律是牛顿以伽俐略的理想斜面实验为基础，总结前人的研究成果加以丰富的想象而提出来的；定律成立的条件是物体不受外力，不能用实验直接验证。

　　 ④牛顿第一定律是牛顿第二定律的基础，不能认为它是牛顿第二定律合外力为零时的特例，第一定律定性地给出了力与运动的关系，第二定律定量地给出力与运动的关系。

　　 (2)惯性：物体保持原来的匀速直线运动状态或静止状态的性质叫做惯性。

　　 ①惯性是物体的固有属性，与物体的受力情况及运动状态无关。

　　 ②质量是物体惯性大小的量度。

　　 ③由牛顿第二定律定义的惯性质量m=F/a和由万有引力定律定义的引力质量严格相等。

　　 ④惯性不是力，惯性是物体具有的保持匀速直线运动或静止状态的性质、力是物体对物体的作用，惯性和力是两个不同的概念。

例1　 气球上吊一重物，以速度从地面匀速竖直上升，经过时间t重物落回地面。不计空气对物体的阻力，重力离开气球时离地面的高度为多少。

解　 方法1：设重物离开气球时的高度为，对于离开气球后的运动过程，可列下面方程：，其中(-h_x表示)向下的位移，为匀速运动的时间，为竖直上抛过程的时间，解方程得：，于是，离开气球时的离地高度可在匀速上升过程中求得，为：

方法2：将重物的运动看成全程做匀速直线运动与离开气球后做自由落体运动的合运动。显然总位移等于零，所以：

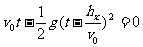
解得：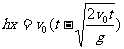

评析　 通过以上两种方法的比较，更深入理解位移规律及灵活运用运动的合成可以使解题过程更简捷。

例2 　两小球以95m长的细线相连。两球从同一地点自由下落，其中一球先下落1s另一球才开始下落。问后一球下落几秒线才被拉直？

解　 方法1：“线被拉直”指的是两球发生的相对位移大小等于线长，应将两球的运动联系起来解，设后球下落时间为ts，则先下落小球运动时间为(t+1)s，根据位移关系有：

解得：t=9s

方法2：若以后球为参照物，当后球出发时前球的运动速度为。以后两球速度发生相同的改变，即前一球相对后一球的速度始终为，此时线已被拉长：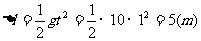

线被拉直可看成前一球相对后一球做匀速直线运动发生了位移：

∴

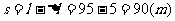
评析　 解决双体或多体问题要善于寻找对象之间的运动联系。解决问题要会从不同的角度来进行研究，如本题变换参照系进行求解。

例3　 如图2-1所示，两个相对斜面的倾角分别为37°和53°，在斜面顶点把两个小球以同样大小的初速度分别向左、向右水平抛出，小球都落在斜面上。若不计空气阻力，则A、B两个小球的运动时间之比为(　　 )

A、1:1　　　 B、4:3　　　 C、16:9　　　 D\9：16

解　 由平抛运动的位移规律可行：

∵　　 ∴

∴

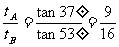
故D选项正确。

评析　 灵活运用平抛运动的位移规律解题，是基本方法之一。应用时必须明确各量的物理意义，不能盲目套用公式。

例4 从空中同一地点沿水平方向同时抛出两个小球，它们的初速度方向相反、大小分别为，求经过多长时间两小球速度方向间的夹角为90°？

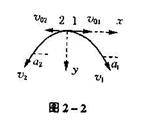
解　 经过时间t，两小球水平分速度、不变，竖直分速度都等于，如图2-2所示，t时刻小球1的速度轴正向夹角为

小球2的速度轴正向夹角为

由图可知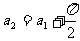　

联立上述三式得　

评析　 弄清平抛运动的性质与平抛运动的速度变化规律是解决本题的关键。

例5　 如图2-3所示，一带电粒子以竖直向上的初速度，自A处进入电场强度为E、方向水平向右的匀强电场，它受到的电场力恰与重力大小相等。当粒子到达图中B处时，速度大小仍为，但方向变为水平向右，那么A、B之间的电势差等于多少？从A到B经历的时间为多长？

解　 带电粒子从A→B的过程中，竖直分速度减小，水平分速度增大，表明带电粒子的重力不可忽略，且带正电荷，受电场力向右。依题意有　

根据动能定理：　

在竖直方向上做竖直上抛运动，则　

解得：。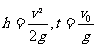

∴

评析　 当带电粒子在电场中的运动不是类平抛运动，而是较复杂的曲线运动时，可以把复杂的曲线运动分解到两个互相正交的简单的分运动来求解。

例6　 如图2-4所示，让一价氢离子、一价氦离子和二价氦离子的混合物由静止经过同一加速电场加速，然后在同一偏转电场里偏转，它们是否会分成三股？请说明理由。

解　 设带电粒子质量为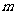、电量为q，经过加速电场加速后，再进入偏转电场中发生偏转，最后射出。设加速电压为　　　 U₁，偏转电压为U₂，偏转电极长为L，两极间距离为d，带电粒子由静止经加速电压加速，则U₁q=，。

带电粒子进入偏转电场中发生偏转，则水平方向上：，

竖直方向上：。

可见带电粒子射出时，沿竖直方向的偏移量与带电粒子的质量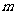和电量q无关。而一价氢离子、一价氦离子和二价氦离子，它们仅质量或电量不相同，都经过相同的加速和偏转电场，故它们射出偏转电场时偏移量相同，因而不会分成三股，而是会聚为一束粒子射出。

评析　 带电粒子在电场中具有加速作用和偏转作用。分析问题时，注意运动学、动力学、功和能等有关规律的综合运用。

3、原来静止的物体受到恒力的作用，物体将向受力的方向做匀加速直线运动；物体受到和初速度方向相同的恒力，物体将做匀速直线运动；物体受到和初速度方向相反的恒力，物体将做匀减速直线运动；若所受到的恒力方向与初速度方向有一定的夹角，物体就做匀变速曲线运动。

2、从动力学上看，物体做匀变速运动的条件是物体受到大小和方向都不变的恒力的作用。匀变速运动的加速度由牛顿第二定律决定。

1、匀变速运动是加速度恒定不变的运动，从运动轨迹来看可以分为匀变速直线运动和匀变速曲线运动。

4、有固定转轴物体的平衡。

例10　 重(N)的由轻绳悬挂于墙上的小球，搁在轻质斜板上，斜板搁于墙角。不计一切摩擦，球和板静止于图1-14所示位置时，图中角均为30°。求：悬线中张力和小球受到的斜板的支持力各多大？小球与斜板接触点应在板上何处？板两端所受压力多大？(假设小球在板上任何位置时，图中角均不变)

解析　 设球与板的相互作用力为N，绳对球的拉力为T，则对球有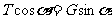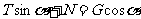，，可得，N=100N。球对板的作用力N、板两端所受的弹力N_A和N_B，板在这三个力作用下静止，则该三个力为共点力，据此可求得球距A端距离，即球与板接触点在板上距A端距离为板长的1/4处。对板，以A端为转动轴，有 对板，以B端为转动轴，有。可得，。