
8.已知双曲线的方程为 , 直线
, 直线 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
解:设A(x1,y1),B(x2,y2),
A到双曲线的左准线x= ─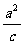 = ─
= ─ 的距离d=|x1+
的距离d=|x1+ |=x1+
|=x1+ ,
,
由双曲线的定义, =e=
=e=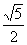 ,
,
∴|AF1|=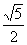 (x1+
(x1+ )=
)=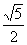 x1+2,
x1+2,
同理,|BF1|=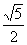 x2+2,
x2+2,
∴|F1A|·|F1B|=(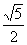 x1+2)(
x1+2)(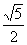 x2+2)=
x2+2)= x1x2+
x1x2+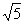 (x1+x2)+4 (1)
(x1+x2)+4 (1)
双曲线的右焦点为F2(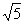 ,0),
,0),
(1)当直线的斜率存在时设直线AB的方程为:y=k(x─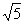 ),
),
由 消去y得 (1─4k2)x2+8
消去y得 (1─4k2)x2+8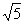 k2x─20k2─4=0,
k2x─20k2─4=0,
∴x1+x2= , x1x2= ─
, x1x2= ─ ,
,
代入(1)整理得
|F1A|·|F1B|= +4=
+4= +4
+4
= +4=
+4=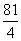 +
+
∴|F1A|·|F1B|>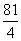 ;
;
(2)当直线AB垂直于x轴时,容易算出|AF2|=|BF2|= ,
,
∴|AF1|=|BF1|=2a+ =
= (双曲线的第一定义), ∴|F1A|·|F1B|=
(双曲线的第一定义), ∴|F1A|·|F1B|=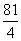
由(1), (2)得:当直线AB垂直于x轴时|F1A|·|F1B| 取最大值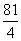
7. (2006江苏)已知三点P(5,2)、 (-6,0)、
(-6,0)、 (6,0).
(6,0).
(Ⅰ)求以 、
、 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、 、
、 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为 、
、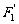 、
、 ,求以
,求以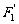 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程。
的双曲线的标准方程。
解:(I)由题意,可设所求椭圆的标准方程为 (a>b>0),
(a>b>0),
其半焦距c=6
2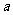 =|PF1|+|PF2|=
=|PF1|+|PF2|=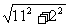 +
+ =6
=6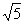
∴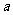 =3
=3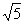 ,b2=a2-c2=45-36=9
,b2=a2-c2=45-36=9
所以所求椭圆的标准方程为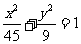
(II)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为P´(2,5)、F1´(0,-6),F2´(0,6)
设所求双曲线的标准方程为 (a1>0,b1>0).
(a1>0,b1>0).
由题意知,半焦距c1=6,
2a1=||P´F1´|-|P´F2´||=|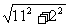 -
- |=4
|=4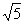 .
.
∴a1=2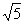 ,b
,b =c
=c -a
-a =36-20=16.
=36-20=16.
所以所求双曲线的标准方程为
6. ||PF1|-|PF2||=6,cos∠F1PF2=
= =
=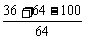 =0
=0
∴∠F1PF2=90°
[解答题]
6.已知双曲线的方程是16x2-9y2=144,F1和F2是双曲线的左、右焦点,点P在双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小
简答提示:1-3.CDC; 4.  ; 5.
; 5.
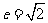 ;
;
5.(2005山东)设双曲线 的右焦点为
的右焦点为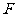 ,右准线
,右准线 与两条渐近线交于P、
与两条渐近线交于P、 两点,如果
两点,如果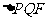 是直角三角形,则双曲线的离心率e=________.
是直角三角形,则双曲线的离心率e=________.
4.(2005福建)已知F1、F2是双曲线 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是_____
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是_____
3. (2005天津)设双曲线以椭圆 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为 ( )
A. B.
B. C.
C.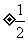 D.
D.
[填空题]
2.(2005湖南)已知双曲线 -
- =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为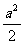 (O为原点),则两条渐近线的夹角为( )
(O为原点),则两条渐近线的夹角为( )
A.30º B.45º C.60º D.90º
1.(2005全国卷II)已知双曲线 的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为 ( )
的焦点为F1、F2,点M在双曲线上且MF1⊥x轴,则F1到直线F2M的距离为 ( )
A. B.
B. C.
C. D.
D.
4.应擅于将几何关系与代数关系相互转化,把平面解析几何问题与向量、平面几何、三角函数、函数、导数、不等式等有机结合相互转化;养成整体处理的习惯。
同步练习 8.2双曲线方程及性质
[选择题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com