1. 证明两平面平行的方法：

　　 (1)利用定义证明。利用反证法，假设两平面不平行，则它们必相交，再导出矛盾。

　　 (2)判定定理：一个平面内有两条相交直线都平行于另一个平面，则这两个平面平行，这个定理可简记为线面平行则面面平行。用符号表示是：

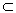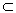　　 a∩b，a α，b α，a∥β，b∥β，则α∥β．

(3)垂直于同一直线的两个平面平行。用符号表示是：a⊥α，a⊥β则α∥β．

(4)平行于同一个平面的两个平面平行 .

4. 两个平面平行的的性质(2)：如果两个平行平面同时和第三个平面相交，那么它们的交线平行.

[附]

3.两个平面平行的性质(1)：如果两个平面平行，那么其中一个平面内的直线平行于另一个平面.

2.两个平面平行的判定定理：如果一个平面内有两条相交直线都平行于一个平面，那么这两个平面平行.

定理的模式：

推论：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面互相平行．

推论模式：

　　　　　　　　 　　　　　　没有公共点--两平面平行

1.两个平面的位置关系有两种：

　　　　　　　　　　 　　　　　有一条公共直线--两平面相交

1.2008年高考材料作文占作文的一半，这种命题形式近年来越来越受到命题人的青睐，其中江西省高考作文题采用了一种特殊的形式来命题--漫画+材料。图画作文在审题上与材料作文稍有不同。这类作文首先要读懂画的内容；依据对图画的理解联系现实，立好意；根据要求行文。

　图画作文的审题方法

3.大自然有晴天雨天，这是人所共知的。其实，你想过没有，不只是大自然有晴天雨天，一个人的生命里同样也会有晴天雨天……

　请以“我的晴天雨天”为话题作文，题目自拟，立意自定，文体不限，不少于800字。

　　[写作提示]

　看到话题以后，我们首先要对话题进行审读、定位。“我的晴天雨天”这个话题，可以从两个层面去理解：一是自然景物，二是生命意义。如果从自然景物的层面去写，就很容易写成纯自然界的晴天雨天，那将意义不大，升华不出寓意深远的主旨，我们应该尽量避免，而要努力地从第二个层面--生命意义去写作。把生命意义的晴天雨天写足写够，自然就有可能写出佳作。

　那么，什么是生命意义的晴天雨天呢？具体说来，生命意义的雨天，可以理解为人生中的坎坷、磨难、挫折、痛苦、打击、失败，等等。生活中，谁的人生会一帆风顺呢？生命意义的晴天，又可以具体理解为高兴、快乐、顺利、上进、收获、成功等。再卑微的生命，也会有高兴、快乐、成功等。从第二个层面去挖掘、生发，是比较容易写出好作文来的。

　此外，还必须注意的一点是，话题中还有一个“我”字，它限定了人物范围，暗示着写自己的亲历、亲受，而避免生拉硬扯，无情造文。

图画作文

10． 如图，已知梯形ABCD中，点E分有向线段所成的比为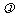，双曲线过C、D、E三点，且以A、B为焦点．当时，求双曲线离心率的取值范围．

解：如图，以AB的垂直平分线为y轴，直线AB为x轴，建立直角坐标系xoy，则CD⊥y轴．

因为双曲线经过点C、D，且以A、B为焦点，由双曲线的对称性知C、D关于x轴对称．依题意，记A(－c，0)，C(，h)，E(x₀, y₀)，其中c=|AB|为双曲线的半焦距，h是梯形的高．

由定比分点坐标公式得

x₀== ，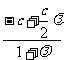

．

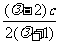设双曲线的方程为，则离心率．

由点C、E在双曲线上，将点C、E的坐标和代入双曲线方程得

，　　　　　　　　　　　 ①

．　　 ②　

由①式得　　 ，　　　　　　　　　　 ③

将③式代入②式，整理得

，

故　　 　　

由题设得，．

解得．

所以双曲线的离心率的取值范围为．　　　

[探索题]如图，在双曲线的上支有三点，它们与点F(0，5)的距离成等差数列。

(1)　　　　　　 求

(2)　　　　　　 证明：线段AC的垂直平分线经过某一定点，并求此点坐标

解：(1)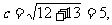故F双曲线的焦点，设准线为，离心率为，

由题设有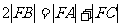　　①

分别过A、B、C作x轴的垂线，则由双曲线的第二定义有，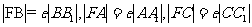

代入①式，得，

于是两边均加上准线与x轴距离的2倍，有

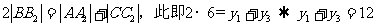
AC的中垂线方程为

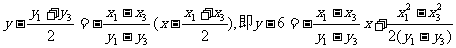　　(2)由于A、C在双曲线上，所以有

相减得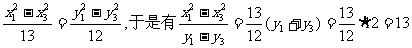

故(2)式化为，易知此直线过定点。

思维点拨：利用第二定义得焦半径，可使问题容易解决，中垂线过弦AC的中点，中点问题往往把A、C的坐标代入方程，两式相减、变形，即可解决问题。

9． 已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为k_PM、k_PN时，那么k_PM与k_PN之积是与点P位置无关的定值试对双曲线C′：－=1写出具有类似特性的性质，并加以证明

解：类似的性质为若MN是双曲线－=1上关于原点对称的两个点，点P是双曲线上任意一点，当直线PM、PN的斜率都存在，并记为k_PM、k_PN时，那么k_PM与k_PN之积是与点P位置无关的定值

设点M的坐标为(m，n)，

则点N的坐标为(－m，－n)，

其中－=1

又设点P的坐标为(x，y)，

由k_PM=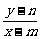，k_PN=，

得k_PM·k_PN=·=，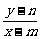

将y²=x²－b²，n²=m²－b²，代入得　 k_PM·k_PN=

点评：本题主要考查椭圆、双曲线的基本性质，考查类比、归纳、探索问题的能力它是一道综合椭圆和双曲线基本知识的综合性题目，对思维能力有较高的要求