赈　 灾 (节选)

钱泳

　 (清)嘉庆十有九年，江南大旱，地势视无锡为高，被灾尤剧。邑侯齐彦槐尝以事赴乡，窃见赤地数千里，民间无米炊，爨(cuān )无薪，汲无水，恻然忧之。夫官发常平仓谷。平粜(tiào )于民，便矣。然远在数千里之外者，不能为升斗之米来也。故官平粜，但能惠近民，不能惠远民。殷富之家，以其余米平粜于其乡，远近咸便矣。然无升斗之资者，不能籴(dí )也。故民平粜，但能惠次贫，不能惠极贫。以此，定图赈之法。至今岁三月，计捐钱十有二晚四千余缗(mín )矣。而殷富之家，好行其德，复于其间为粥以赈，城乡设厂十余处，计所捐又不下万数千缗，饥民赖以全活者无算。呜呼，孰谓人心之淳，风俗之厚，今不若古哉！

8．解释下列句中加点的词。(4分)

　 (1)嘉庆十有九年　 　　　　　　　　　(2)窃见赤地数千里 　　　　　　　　

(3)爨(cuān )无薪 　　　　　　　　　(4)远近咸便矣　 　　　　　　　　

12.已知集合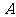和集合各含有12个元素，含有4个元素，求同时满足下面两个条件的集合的个数：(1)，且中含有3个元素；(2)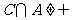(为空集)．

　 分析　 该题是1986年的高考题，本题形式是集合,实质是计数问题,要用排列组合的方法求解.如图所示，中的三个元素的取法不止一类，可考虑分类解之．

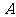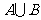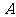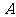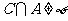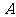　　 解　 因为、各有12个元素，含有4个元素，所以中元素的个数是(个). 其中，属于的元素有12个，属于而不属于的元素有8个，要使，则组成中的元素至少有一个含在中，集合的个数是

　 1)只含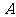中1个元素的有个．

　 2)含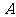中2个元素的有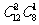个；

　 3)含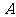中3个元素的有个.

　 故所求的集合C的个数共有　 ++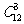=1084(个)．

[探索题]某篮球队共7名老队员，5名新队员，根据下列情况分别求出有多少种不同的出场阵容.

(1)某老队员必须上场，某2新队员不能出场；

(2)有6名打前锋位，4名打后卫位，甲、乙两名既能打前锋又能打后卫位.

解：(1)C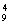=126种.

(2)以2名既擅长前锋位又能打后卫位的队员是否上场，且上场后是前锋还是后卫作分类标准：①甲、乙都不上场有CC=120种；②甲、乙有一名上场，作前锋位有C(CC)种，作后卫位有C(CC)种，共C(CC)+C(CC)=340种；③甲、乙都上场，有CC+CC+C(CC)=176种.据分类计数原理，共有120+340+176=636种.

11.从1，2，…，30这前30个自然数中，每次取不同的三个数，使这三个数的和是3的倍数的取法有多少种？

解：令A＝{1，4，7，10，…，28}，B＝{2，5，8，11，…29}，C＝{3，6，9，…，30}组成四位数的方式有以下四类符合题意：①A，B，C中各取一个数，有种；②仅在A中取3个数，有种；③仅在B中取3个数，有种；④仅在C中取3个数，有种，故由加法原理得：＝1360种．