
2.I cannot find my watch;I must have l________ it.
1.I admire Einstein because he was a mathematical ________(天才).
4.圆与圆的位置关系:依平面几何的圆心距|O1O2|与两半径r1 ,r2 的和差关系判定.
(1)设⊙O1 圆心O1 ,半径r1 ,⊙O2 圆心O2 ,半径r2 则:
①当r1 +r2 =|O1O2|时⊙O1 与⊙O2 外切;②当|r1 -r2|=|O1O2| 时,两圆相切;③当|r1 -r2
时,两圆相切;③当|r1 -r2 |
| <|O1O2|<r1 +r2 时两圆相交;④当|r1 -r2|>|O1O2|时两圆内含;⑤当r1 +r2 <|O1O2|时两圆外离
<|O1O2|<r1 +r2 时两圆相交;④当|r1 -r2|>|O1O2|时两圆内含;⑤当r1 +r2 <|O1O2|时两圆外离
(2)设⊙O1 :x2 +y2 +D1x +E1y +F1 =0,⊙O2 :x2 +y2 +D2x +E2y +F2 =0。
①两圆相交A 、B 两点,其公共弦所在直线方程为(D1 -D2)x +(E1 -E2)y +F1 -F2 =0;
②经过两圆的交点的圆系方程为x2 +y2 +D1x +E1y +F1 +l(x2 +y2 +D2x +E2y +F2)=0(不包括⊙O2 方程)
3.直线与圆的位置关系:l :f1(x ,y)=0.圆C :f2(x ,y)=0消y 得F(x2)=0。
(1)直线与圆相交:F(x ,y)=0中D >0;或圆心到直线距离d <r 。
直线与圆相交的相关问题:①弦长|AB|=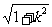 ·|x1 -x2|=
·|x1 -x2|= ·
· ,或|AB|=2
,或|AB|=2 ;②弦中点坐标(
;②弦中点坐标(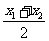 ,
, );③弦中点轨迹方程。
);③弦中点轨迹方程。
(2)直线与圆相切:F(x)=0中D =0,或d =r .其相关问题是切线方程.如P(x0 ,y0)是圆x2 +y2 =r2 上的点,过P 的切线方程为x0x +y0y =r2 ,其二是圆外点P(x0 ,y0)向圆到两条切线的切线长为 或
或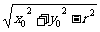 ;其三是P(x0 ,y0)为圆x2 +y2 =r2 外一点引两条切线,有两个切点A ,B ,过A ,B 的直线方程为x0x +y0y =r2 。
;其三是P(x0 ,y0)为圆x2 +y2 =r2 外一点引两条切线,有两个切点A ,B ,过A ,B 的直线方程为x0x +y0y =r2 。
(3)直线与圆相离:F(x)=0中D <0;或d <r ;主要是圆上的点到直线距离d 的最大值与最小值,设Q 为圆C :(x -a) 2 +(y -b) 2 =r2 上 任一点,|PQ|max =|PC|+r ;|PQ|min =|PQ|-r ,是利用图形的几何意义而不是列出距离的解析式求最值.
任一点,|PQ|max =|PC|+r ;|PQ|min =|PQ|-r ,是利用图形的几何意义而不是列出距离的解析式求最值.
1.关于直线对称问题:
(1)关于l :Ax +By +C =0对称问题:不论点,直线与曲线关于l 对称问题总可以转化为点关于l 对称问题,因为对称是由平分与垂直两部分组成,如求P(x0 ,y0)关于l :Ax +By +C =0对称点Q(x1 ,y1).有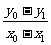 =-
=- (1)与A·
(1)与A·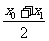 +B·
+B· +C =0。
+C =0。
(2)解出x1 与y1 ;若求C1 :曲线f(x ,y)=0(包括直线)关于l :Ax +By +C1 =0对称的曲线C2 ,由上面的(1)、(2)中求出x0 =g1(x1 ,y1)与y0 =g2(x1 ,y1),然后代入C1 :f [g1(x1 ,y1),g2(x2 ,y2)]=0,就得到关于l 对称的曲线C2 方程:f [g1(x ,y),g2(x ,y)]=0。
(3)若l :Ax +By +C =0中的x ,y 项系数|A|=1,|B |=1.就可以用直接代入解之,尤其是选择填空题。如曲线C1 :y2 =4 x -2关于l :x -y -4=0对称的曲线l2 的方程为:(x -4) 2 =4(y +4)-2.即y 用x -4代 ,x 用y +4代,这样就比较简单了
,x 用y +4代,这样就比较简单了
(4)解有关入射光线与反射光线问题就可以用对称问题来解决
点与圆位置关系:P(x0 ,y0)和圆C :(x -a) 2 +(y -b) 2 =r2。
①点P 在圆C 外有(x0 -a) 2 +(y0 -b) 2 >r2;
②点P 在圆上:(x0 -a) 2 +(y0 - b) 2
=r2;
b) 2
=r2;
③点P 在圆内:(x0 -a) 2 +(y0 -b) 2 <r2 。
题型1:直线间的位置关系
例1.(全国Ⅱ文15)已知圆O: 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的 三角形的面积等于
三角形的面积等于
[解析]由题意可直接求出切线方程为y-2=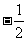 (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和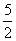 ,所以所求面积为
,所以所求面积为 。
。
[答案] 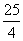
[总结点评]本题主要考查直线的方程、直线与圆的位置关系等知识,数形结合与分类讨论的思想方法,以及定性地分析问题和解决问题的能力.
(2)已知两条直线 若
若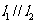 ,则
,则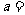 ___ _。
___ _。
解 析:(1)答案:
析:(1)答案: ;(2)2。
;(2)2。
点评:(1)三点共线问题借助斜率来解决,只需保证 ;(2)对直线平行关系的判断在一般式方程中注意系数为零的情况。
;(2)对直线平行关系的判断在一般式方程中注意系数为零的情况。
例2.已知两条直线 和
和 互相垂直,则
互相垂直,则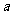 等于(
)
等于(
)
A.2 B.1 C.0 D.
(2)(2007安徽理,7)
若曲线 的一条切线
的一条切线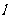 与直线
与直线
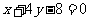 垂直,则
垂直,则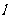 的方程为( )
的方程为( )
A.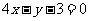 B.
B.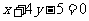 C.
C. D.
D.
解析:(1)答案为D;(2)与直线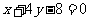 垂直的直线
垂直的直线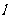 为
为 ,即
,即 在某一点的导数为4,而
在某一点的导数为4,而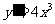 ,所以
,所以 在(1,1)处导数为4,此点的切线为
在(1,1)处导数为4,此点的切线为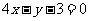 ,故选A。
,故选A。
点评:直线间的垂直关系要充分利用好斜率互为负倒数的关系,同时兼顾到斜率为零和不存在两种情况。
题型2:距离问题
例3. 将直线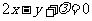 沿
沿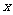 轴向左平移1个单位,所得直线与圆
轴向左平移1个单位,所得直线与圆 相切,则实数
相切,则实数 的值为
( )
的值为
( )
(A)-3或7 (B)-2或8 (C)0或10 (D)1或11
[思路点拨]本题考查了平移公式、直线与圆的位置关系,只要正确理解平移公式和直线与圆相切的充要条件就可解决.
[正确解答]由题意可知:直线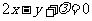 沿
沿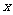 轴向左平移1个单位后的直线
轴向左平移1个单位后的直线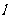 为:
为:
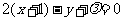 .已知圆的圆心为
.已知圆的圆心为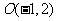 ,半径为
,半径为 .
.
解法1:直线与圆相切,则圆心到直线的距离等于圆的半径,因而有
 ,得
,得 或7.
或7.
解法2:设切点为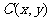 ,则切点满足
,则切点满足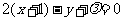 ,即
,即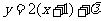 ,代入圆方程整理得:
,代入圆方程整理得: , (*)
, (*)
由直线与圆相切可知,(*)方程只有一个解,因而有 ,得
,得 或7.
或7.
解法3:由直线与圆相切,可知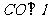 ,因而斜率相乘得-1,即
,因而斜率相乘得-1,即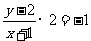 ,又因为
,又因为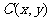 在圆上,满足方程
在圆上,满足方程 ,解得切点为
,解得切点为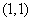 或
或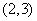 ,又
,又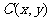 在直线
在直线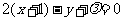 上,解得
上,解得 或7.
或7.
(2)(湖北文14)过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,
则线段PQ的长为 。
[解析]可得圆方程是 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得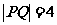 .
.
例4。 (圆、向量与三角函数)
设A、B为圆 上两点,O为坐标原点(A、O、B不共线)
上两点,O为坐标原点(A、O、B不共线)
(Ⅰ)求证: 垂直.
垂直.
(Ⅱ)当 时.求
时.求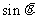 的值.
的值.
解:(Ⅰ)由 [来源:]
[来源:]
则

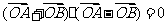
则 垂直
垂直
(Ⅱ)由
又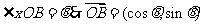
由
即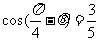

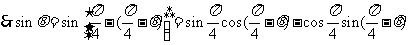
=
点评:该题全面综合了解析几何、平面几何、代数的相关知识,充分体现了“注重学科知识的内在联系”.题目的设计新颖脱俗,能较好地考查考生综合运用数学知识解决问题的能力.比较深刻地考查了解析法的原理和应用,以及分类讨论的思想、方程的思想。该题对思维的目的性、逻辑性、周密性、灵活性都进行了不同程度的考查.对运算、化简能力要求也较高,有较好的区分度
题型3:直线与圆的位置关系
例5.(2009江苏卷18)(本小题满分16分)
 在平面直角坐标系
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线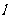 过点
过点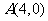 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线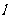 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线 和
和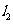 ,它们分别与圆
,它们分别与圆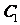 和圆
和圆 相交,且直线
相交,且直线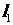 被圆
被圆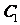 截得的弦长与直线
截得的弦长与直线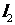 被圆
被圆 截得的弦长相等,试求所有满足条
截得的弦长相等,试求所有满足条 件的点P的坐标
件的点P的坐标
解 (1)设直线 的方程为:
的方程为: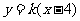 ,即
,即
由垂径定理,得:圆心 到直线
到直线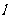 的距离
的距离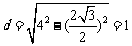 ,
,
结合点到直线距离公式,得:
化简得: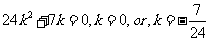
求直线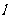 的方程为:
的方程为: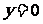 或
或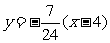 ,即
,即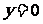 或
或
(2) 设点P坐标为 ,直线
,直线 、
、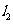 的方程分别为:
的方程分别为:
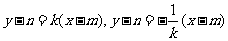 ,即:
,即:
因为直线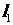 被圆
被圆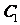 截得的弦长与直线
截得的弦长与直线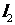 被圆
被圆 截得的弦长相等,两圆半径相等。
截得的弦长相等,两圆半径相等。
由垂径定理,得::圆心 到直线
到直线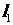 与
与 直线
直线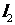 的距离相等。
的距离相等。
故有: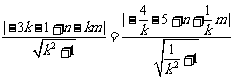 ,
,
化简得: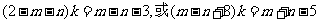
关于 的方程有无穷多解,有:
的方程有无穷多解,有: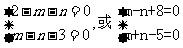
解之得:点P坐标为 或
或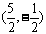 。
。
例6.已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
(A) 对任意实数k与q,直线l和圆M相切;
(B) 对任意实数k与q,直线l和圆M有公共点;
(C) 对任意实数q,必存在实数k,使得直线l与和圆M相切;
(D)对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)
解析:圆心坐标为(-cosq,sinq)
d=
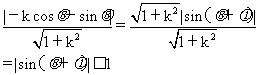
故选(B)(D)
点评:该题复合了三角参数的形式,考察了分类讨论的思想。
题型4:直线与圆综合问题
例7.(江西理16).设直线系 ,对于下列四个命题:
,对于下列四个命题:
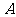 .
. 中所有直线均经过一个定点
中所有直线均经过一个定点
 .存在定点
.存在定点 不在
不在 中的任一条直线上
中的任一条直线上
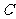 .对于任意整数
.对于任意整数 ,存在正
,存在正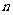 边形,其所有边均在
边形,其所有边均在 中的直线上
中的直线上
 .
. 中的直线所
中的直线所 能围成的正三角形面积都相等
能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
[解析]因为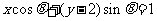 所以点
所以点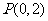 到
到 中每条直线的距离
中每条直线的距离
即 为圆
为圆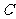 :
: 的全体切线组成的集合,从而
的全体切线组成的集合,从而 中存在两条平行直线,
中存在两条平行直线,
所以A错误;
又因为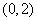 点不存在任何直线上,所以B正确;
点不存在任何直线上,所以B正确;
对任意 ,存在正
,存在正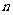 边形使其内切圆为圆
边形使其内切圆为圆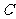 ,故
,故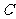 正确;
正确;
 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形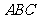 和
和 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C.
[答案]
例8.(江西理16).设直线系 ,对于下列四个命题:
,对于下列四个命题:
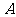 .
. 中所有直线均经过一个定点
中所有直线均经过一个定点
 .存在定点
.存在定点 不在
不在 中的任一条直线上
中的任一条直线上
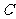 .对于任意整数
.对于任意整数 ,存在正
,存在正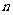 边形,其所有边均在
边形,其所有边均在 中的直线上
中的直线上
 .
. 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
[解析]因为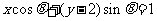 所以点
所以点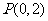 到
到 中每条直线的距离
中每条直线的距离
即 为圆
为圆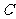 :
: 的全体切线组成的集合,从而
的全体切线组成的集合,从而 中存在两条平行直线,
中存在两条平行直线,
所以A错误;
又因为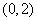 点不存在任何直线上,所以B正确;
点不存在任何直线上,所以B正确;
对任意 ,存在正
,存在正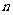 边形使其内切圆为圆
边形使其内切圆为圆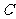 ,故
,故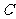 正确;
正确;
 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形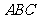 和
和 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C.
[答案]
例9.(江西理16).设直线系 ,对于下列四个命题:
,对于下列四个命题:
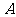 .
. 中所有直线均经过一个定点
中所有直线均经过一个定点
 .存在定点
.存在定点 不在
不在 中的任一条直线上
中的任一条直线上
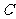 .对于任意整数
.对于任意整数 ,存在正
,存在正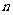 边形,其所有边均在
边形,其所有边均在 中的直线上
中的直线上
 .
. 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
[解析]因为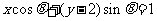 所以点
所以点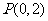 到
到 中每条直线的距离
中每条直线的距离
即 为圆
为圆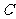 :
: 的全体切线组成的集合,从而
的全体切线组成的集合,从而 中存在两条平行直线,
中存在两条平行直线,
所以A错误;
又因为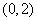 点不存在任何直线上,所以B正确;
点不存在任何直线上,所以B正确;
对任意 ,存在正
,存在正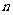 边形使其内切圆为圆
边形使其内切圆为圆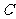 ,故
,故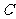 正确;
正确;
 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形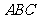 和
和 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C.
[答案]
例10.已知函数f(x)=x2-1(x≥1)的图像为C1,曲线C2与C1关于直线y=x对称。
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,x1,x2 ∈M,且x1≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
∈M,且x1≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A、B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
解析:(1)曲线C1和C2关于直线y=x对称,则g(x)为f(x)的反函数。
∵y=x2-1,x2=y+1,又x≥1,∴x= ,则曲线C2的方程为g(x)=
,则曲线C2的方程为g(x)= 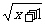 (x≥0)。
(x≥0)。
(2)设x1,x2∈M,且x1≠x2,则x1-x2≠0。又x1≥0, x2≥0,
∴|g(x1)-g(x2)|=| 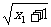 -
-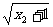 |=
|= ≤
≤ <|x1-x2|。
<|x1-x2|。
(3)设A(x1,y1)、B(x2,y2)为曲线C2上任意不同两点,x1,x2∈M,且x1≠x2,
由(2)知,|kAB|=| |=
|=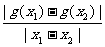 <1
<1
∴直线AB的斜率|kAB|≠1,又直线y=x的斜率为1,∴直线AB与直线y=x必相交。
 点评:曲线对称问题应从方程与曲线的对应关系入手来处理,最终转化为点的坐标之间的对应关系
点评:曲线对称问题应从方程与曲线的对应关系入手来处理,最终转化为点的坐标之间的对应关系
题型6:轨迹问题
例11.已知动圆过定点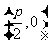 ,且与直线
,且与直线 相切,其中
相切,其中 。
。
(I)求动圆圆心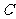 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹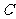 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线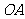 和
和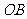 的倾斜角分别为
的倾斜角分别为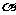 和
和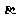 ,当
,当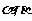 变化且
变化且 为定值
为定值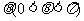 时,证明直线
时,证明直线 恒过定点,并求出该定点的坐标。
恒过定点,并求出该定点的坐标。
解析:(I)如图,设 为动圆圆心,
为动圆圆心,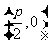 为记为
为记为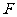 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为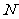 ,由题意知:
,由题意知: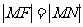 即动点
即动点 到定点
到定点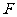 与定直线
与定直线 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点 的轨迹为抛物线,其中
的轨迹为抛物线,其中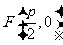 为焦点,
为焦点, 为准线,所以轨迹方程为
为准线,所以轨迹方程为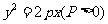 ;
;
(II)如图,设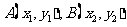 ,由题意得
,由题意得 (否则
(否则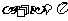 )且
)且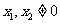 所以直线
所以直线 的斜率存在,设其方程为
的斜率存在,设其方程为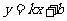 ,显然
,显然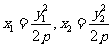 ,将
,将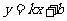 与
与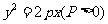 联立消去
联立消去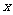 ,得
,得 由韦达定理知
由韦达定理知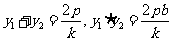 ①
①
(1)当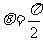 时,即
时,即 时,
时, 所以
所以 ,
, 所以
所以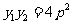 由①知:
由①知: 所以。因此直线
所以。因此直线 的方程可表示为
的方程可表示为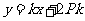 ,即
,即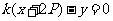 ,所以直线
,所以直线 恒过定点
恒过定点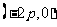 。
。
(2)当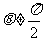 时,由
时,由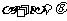 ,
,
得 =
= =
=
 ,
,
将①式代入上式整理化简可得: ,所以
,所以 ,
,
此时,直线 的方程可表示为
的方程可表示为
 即
即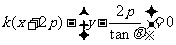 ,所以直线
,所以直线 恒过定点
恒过定点 。
。
所以由(1)(2)知,当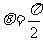 时,直线
时,直线 恒过定点
恒过定点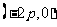 ,当
,当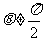 时直线
时直线 恒过定点
恒过定点 。
。
点评:该题是圆与圆锥曲线交汇题目,考察了轨迹问题,属于难度较大的综合题目。
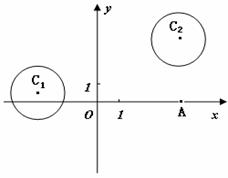
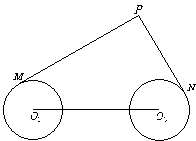 例12.如图,圆
例12.如图,圆 与圆
与圆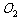 的半径都是1,
的半径都是1,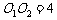 . 过动点
. 过动点 分别作圆
分别作圆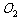 、圆
、圆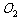 的切线
的切线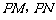 (
( 分别为切点),使得
分别为切点),使得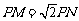 . 试建立适当的坐标系,并求动点
. 试建立适当的坐标系,并求动点 的轨迹方程
的轨迹方程
解析:以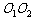 的中点
的中点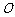 为原点,
为原点,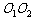 所在直线为
所在直线为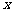 轴,建立如图所示的平面直角坐标系,则
轴,建立如图所示的平面直角坐标系,则 ,
,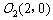 。
。
由已知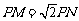 ,得
,得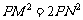 。
。
因为两圆半径均为1,所以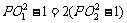 。
。
设 ,则
,则 ,
,
即 (或
(或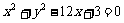 )。
)。
点评:本小题主要考查求轨迹方程的方法及基本运算能力
题型7:课标创新题
例13.已知实数x、y满足 ,求
,求 的最大值与最小值。
的最大值与最小值。
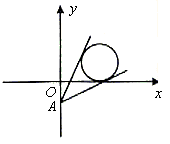 解析:
解析: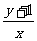 表示过点A(0,-1)和圆
表示过点A(0,-1)和圆 上的动点(x,y)的直线的斜率。
上的动点(x,y)的直线的斜率。
如下图,当且仅当直线与圆相切时,直线的斜率分别取得最大值和最小值
设切线方程为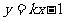 ,即
,即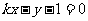 ,则
,则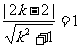 ,解得
,解得 。
。
因此,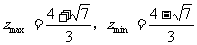
点评:直线知识是解析几何的基础知识,灵活运用直线知识解题具有构思巧妙、直观性强等特点,对启迪思维大有裨益。下面举例说明其在最值问题中的巧妙运用
例14.设双曲线 的两支分别为
的两支分别为 ,正三角形PQR的三顶点位于此双曲线上。若
,正三角形PQR的三顶点位于此双曲线上。若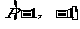 在
在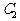 上,Q、R在
上,Q、R在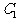 上,求顶点Q、R的坐标
上,求顶点Q、R的坐标

分析:正三角形PQR中,有 , 则以
, 则以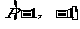 为圆心,
为圆心,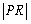 为半径的圆与双曲线交于R、Q两点。
为半径的圆与双曲线交于R、Q两点。
根据两曲线方程可求出交点Q、R坐标
解析:设以P为圆心,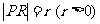 为半径的圆的方程为:
为半径的圆的方程为: ,
,
由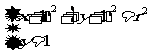 得:
得: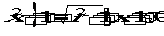 。 (其中,可令
。 (其中,可令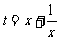 进行换元解之)
进行换元解之)
设Q、R两点的坐标分别为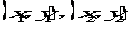 ,则
,则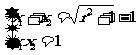 。
。
即 ,
,
同理可得: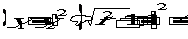 , 且因为△PQR是正三角形,则
, 且因为△PQR是正三角形,则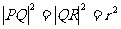 ,
,
即 ,得
,得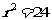 。
。
代入方程 ,即
,即 。
。
由方程组 ,得:
,得: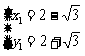 或
或 ,
,
所以,所求Q、R的坐标分别为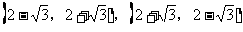
点评:圆是最简单的二次曲线,它在解析几何及其它数学分支中都有广泛的应用。对一些数学问题,若能作一个辅助圆,可以沟通题设与结论之间的关系,从而使问题得解,起到铺路搭桥的作用
4.两圆位置关系的判定方法
设两圆圆心分别为O1,O2,半径分别为r1,r2, 。
。
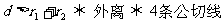 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
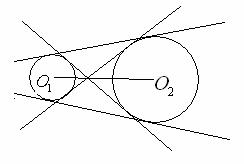

外离 外切

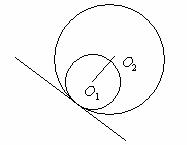

相交 内切 内含
判断两个圆的位置关系也可以通过联立方程组判断公共解的个数来解决
3.直线 与圆
与圆 的位置关系有三种
的位置关系有三种
(1)若 ,
, ;
;
(2)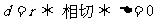 ;
;
(3) 。
。
还可以利用直线方程与圆的方程联立方程组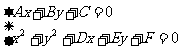 求解,通过解的个数来判断:
求解,通过解的个数来判断:
(1)当方程组有2个公共解时(直线与圆有2个交点),直线与圆相交;
(2)当方程组有且只有1个公共解时(直线与圆只有1个交点),直线与圆相切;
(3)当方程组没有公共解时(直线与圆没有交点),直线与圆相离;
即:将直线方程代入圆的方程得到一元二次方程,设它的判别式为Δ,圆心C到直线l的距离为d,则直线与圆的位置关系满足以下关系:
相切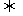 d=r
d=r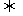 Δ=0;
Δ=0;
相交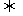 d<r
d<r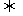 Δ>0;
Δ>0;
相离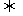 d>r
d>r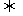 Δ<0。
Δ<0。
2. 距离
(1)两点间距离:若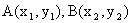 ,则
,则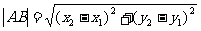
特别地: 轴,则
轴,则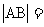
 、
、 轴,则
轴,则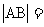
 。
。
(2)平行线间距离:若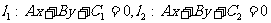
 ,
,
则: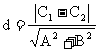 。注意点:x,y对应项系数应相等
。注意点:x,y对应项系数应相等
(3)点到直线的距离: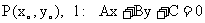 ,则P到l的距离为:
,则P到l的距离为: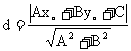
1.直线l1与直线l2的的平行与垂直
(1)若l1,l2均存在斜率且不重合:
①l1//l2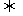 k1=k2;②l1
k1=k2;②l1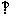 l2
l2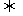 k1k2=-1。
k1k2=-1。
(2)若
若A1、A2、B1、B2都不为零。
①l1//l2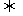
 ;
;
②l1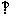 l2
l2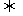 A1A2+B1B2=0;
A1A2+B1B2=0;
③l1与l2相交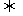
 ;
;
④l1与l2重合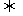
 ;
;
注意:若A2或B2中含有字母,应注意讨论字母=0与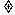 0的情况。两条直线的交点:两条直线的交点的个数取决于这两条直线的方程组成的方程组的解的个数
0的情况。两条直线的交点:两条直线的交点的个数取决于这两条直线的方程组成的方程组的解的个数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com