(三)课堂小结

1．在只有重力做功的过程中，物体的机械能总量不变。通过例题分析要加深对机械能守恒定律的理解。

2．应用机械能守恒定律解决问题时，应首先分析物体运动过程中是否满足机械能守恒条件，其次要正确选择所研究的物理过程，正确写出初、末状态物体的机械能表达式。

3．从功和能的角度分析、解决问题，是物理学研究的重要方法和途径。通过本节内容的学习，逐步培养用功和能的观点分析解决物理问题的能力。

4．应用功和能的观点分析处理的问题往往具有一定的综合性，例如与圆周运动或动量知识相结合，要注意将所学知识融汇贯通，综合应用，提高综合运用知识解决问题的能力。

(二)进行新课：

1．只有重力对物体做功时物体的机械能守恒

问题：质量为m的物体自由下落过程中，经过高度h₁处速度为v₁，下落至高度h₂处速度为v₂，不计空气阻力，分析由h₁下落到h₂过程中机械能的变化(引导学生思考分析)。

分析：根据动能定理，有

下落过程中重力对物体做功，重力做功在数值上等于物体重力势能的变化量。取地面为参考平面，有

W_G＝mgh₁-mgh₂

由以上两式可以得到

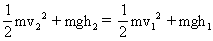
引导学生分析上面式子所反映的物理意义，并小结：下落过程中，物体重力势能转化为动能，此过程中物体的机械能总量不变。

指出问题：上述结论是否具有普遍意义呢？作为课后作业，请同学们课后进一步分析物体做平抛和竖直上抛运动时的情况。

明确：可以证明，在只有重力做功的情况下，物体动能和势能可以相互转化，而机械能总量保持不变。(使学生充分理解机械能守恒的条件)

提出问题：在只有弹簧弹力做功时，物体的机械能是否变化呢？

2．弹簧和物体组成的系统的机械能

以弹簧振子为例(未讲振动，不必给出弹簧振子名称，只需讲清系统特点即可)，简要分析系统势能与动能的转化。

明确：进一步定量研究可以证明，在只有弹簧弹力做功条件下，物体的动能和弹簧的弹性势能可以相互转化，系统的机械能总量不变。

问题：如图，小球自a点由静止自由下落，到b点时与弹簧接触，到c点时弹簧被压缩到最短，若不计弹簧质量和空气阻力，在小球由a→b→c的运动过程中

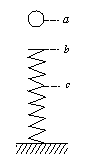
图1-17-3

A．小球和弹簧总机械能守恒

B．小球的重力势能随时间均匀减少

C．小球在b点时动能最大

D．到c点时小球重力势能的减少量等于弹簧弹性势能的增加量

(AD)

3．机械能守恒定律的综合应用

[例1]在距离地面20m高处以15m/s的初速度水平抛出一小球，不计空气阻力，取g＝10m/s²，求小球落地速度大小。

引导学生思考分析，提出问题：

(1)前面学习过应用运动合成与分解的方法处理平抛运动，现在能否应用机械能守恒定律解决这类问题？

(2)小球抛出后至落地之前的运动过程中，是否满足机械能守恒的条件？如何应用机械能守恒定律解决问题？

归纳学生分析的结果，明确：

(1)小球下落过程中，只有重力对小球做功，满足机械能守恒条件，可以用机械能守恒定律求解；

(2)应用机械能守恒定律时，应明确所选取的运动过程，明确初、末状态小球所具有的机械能。

例题求解过程：

取地面为参考平面，抛出时小球具有的重力势能E_p1＝mgh，动能

落地时小球的速度大小为

提出问题：请考虑用机械能守恒定律解决问题与用运动合成解决问题的差异是什么？

[例2]小球沿光滑的斜轨道由静止开始滑下，并进入在竖直平面内的离心轨道运动，如图所示，为保持小球能够通过离心轨道最高点而不落下来，求小球至少应从多高处开始滑下？已知离心圆轨道半径为R，不计各处摩擦。

提出问题，引导学生思考分析：

(1)小球能够在离心轨道内完成完整的圆周运动，对小球通过圆轨道最高点的速度有何要求？

(2)从小球沿斜轨道滑下，到小球在离心轨道内运动的过程中，小球的机械能是否守恒？

(3)如何应用机械能守恒定律解决这一问题？如何选取物体运动的初、末状态？

归纳学生分析的结果，明确：

(1)小球能够通过圆轨道最高点，要求小球在最高点具有一定速度，即此时小球运动所需要的向心力，恰好等于小球所受重力；

(2)运动中小球的机械能守恒；

(3)选小球开始下滑为初状态，通过离心轨道最高点为末状态，研究小球这一运动过程。

例题求解过程：

取离心轨道最低点所在平面为参考平面，开始时小球具有的机械能E₁＝mgh。通过离心轨道最高点时，小球速度为v，此时小球的机械能

成完整的圆周运动。

进一步说明：在中学阶段，由于数学工具的限制，我们无法应用牛顿运动定律解决小球在离心圆轨道内的运动。但应用机械能守恒定律，可以很简单地解决这类问题。

[例3]长l＝80cm的细绳上端固定，下端系一个质量 m＝100g的小球。将小球拉起至细绳与竖直方向成60°角的位置，然后无初速释放。不计各处阻力，求小球通过最低点时，细绳对小球拉力多大？取g＝10m/s²。

提出问题，引导学生分析思考：

(1)释放后小球做何运动？通过最低点时，绳对小球的拉力是否等于小球的重力？

(2)能否应用机械能守恒定律求出小球通过最低点时的速度？

归纳学生分析结果，明确：

(1)小球做圆周运动，通过最低点时，绳的拉力大于小球的重力，此二力的合力等于小球在最低点时所需向心力；

(2)绳对小球的拉力不对小球做功，运动中只有重力对球做功，小球机械能守恒。

例题求解过程：

小球运动过程中，重力势能的变化量ΔE_p＝-mgh＝-mgl(1-cos60°)，

在最低点时绳对小球的拉力大小为

提出问题：通过以上各例题，总结应用机械能守恒定律解决问题的基本方法。

归纳学生的分析，作课堂小结。

(一)复习引入新课

上节课讲了机械能守恒定律：在只有重力做功的情形下，物体的动能和势能可以发生相互转化，但机械能的总量保持不变。并学习了应用机械能守恒定律解答简单力学问题。本节课我们用上节课学习的机械能守恒定律来解答较复杂的力学问题。

同学们回忆一下利用机械能守恒定律的解题步骤：

①选取研究对象----物体系或物体。

②根据研究对象所经历的物理过程，进行受力，做功分析，判断机械能是否守恒。

③恰当地选取参考平面，确定研究对象在过程的初、末态时的机械能。

④根据机械能守恒定律列方程，进行求解。

多媒体设备

讲授、讨论、练习、多媒体辅助教学

3．能否正确选用机械能守恒定律解决问题是本节学习的另一难点。通过本节学习应让学生认识到，从功和能的角度分析、解决问题是物理学的重要方法之一；同时进一步明确，在对问题作具体分析的条件下，要能够正确选用适当的物理规律分析、处理问题。

2．分析物体系统所具有的机械能，尤其是分析、判断物体所具有的重力势能，是本节学习的难点之一。在教学中应让学生认识到，物体重力势能大小与所选取的参考平面(零势面)有关；而重力势能的变化量是与所选取的参考平面无关的。在讨论物体系统的机械能时，应先确定参考平面。

1．机械能守恒定律是本章教学的重点内容，本节教学的重点是使学生掌握物体系统机械能守恒的条件；能够正确分析物体系统所具有的机械能；能够应用机械能守恒定律解决有关问题。

3．学习从功和能的角度分析、处理问题的方法，提高运用所学知识综合分析、解决问题的能力。

2．会用机械能守恒定律解决力学问题，知道应用这个定律的解题步骤，知道用这个定律处理问题的优点．