
物体受到多个力作用时求其合力,可将各个力沿两个相互垂直的方向直行正交分解,然后再分别沿这两个方向求出合力,正交分解法是处理多个力作用用问题的基本方法,步骤为:
①正确选择直角坐标系,一般选共点力的作用点为原点,水平方向或物体运动的加速度方向为X轴,使尽量多的力在坐标轴上。
②正交分解各力,即分别将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。
Fx=F1x+F2x+…+Fnx Fy=F1y+F2y+…+Fny
③共点力合力的大小为F= ,合力方向与X轴夹角
,合力方向与X轴夹角
规律方法1、基本规律与方法的应用
[例1]两个力的合力与这两个力的关系,下列说法中正确的是:( CD )
A、 合力比这两个力都大
B、 合力至少比两个力中较小的力大
C、 合力可能比这两个力都小
D、 合力可能比这两个力都大
解析:(1)公式法:由合力公式F= 得
得
① 当θ=00时,F=F1+F2;②当θ=1800时,F=|F1-F2|;③当θ=900时,F=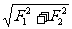 ;④当θ=1200且F1=F2时,F=F1=F2
;④当θ=1200且F1=F2时,F=F1=F2
可见合力可能比任何一个分力都大,也可能比任何一个分力都小,也可能等于每一个分力
(2)图象法:由三角形定则知,合力与分力的关系实际上是三角形的一个边与其它两个边的关系。由两边之和大于第三边,两边之差小于第三边,同时考虑到两个分力同向或反向的情况,合力的取值范围为| F1-F2|≤F≤(F1+F2),故答案为CD
 [例2]施用一动滑轮将一物体提起来,不计滑轮与绳的质量及其间的摩擦力,则(BCD)
[例2]施用一动滑轮将一物体提起来,不计滑轮与绳的质量及其间的摩擦力,则(BCD)
A.总可以省力一半; B.最大省力一半;
C.拉力可能大于被提物体的重量; D.拉力可能等于被提物体的重量;
解析:如图1-21所示,当拉力沿竖直方向时.省力一半,当沿2的方向上提时拉力肯定大于物体重力一半.所以A错B对,当两绳间夹角等于1200时拉力等于物体重量,所以D对,当夹角大于1200时,拉力大于物体重量,所以c对.
 说明:力是矢量,它的加减不是简单的代数加减;不共线的两个共点力与它们的合力构成三角形,利用正、余弦定理,三角形几何知识来分析相关问题,直观简捷!
说明:力是矢量,它的加减不是简单的代数加减;不共线的两个共点力与它们的合力构成三角形,利用正、余弦定理,三角形几何知识来分析相关问题,直观简捷!
[例3] A的质量是m,A、B始终相对静止,共同沿水平面向右运动。当a1=0时和a2=0.75g时,B对A的作用力FB各多大?
 解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
当a1=0时,G与 FB二力平衡,所以FB大小为mg,方向竖直向上。
当a2=0.75g时,用平行四边形定则作图:先画出重力(包括大小和方向),再画出A所受合力F的大小和方向,再根据平行四边形定则画出FB。由已知可得FB的大小FB=1.25mg,方向与竖直方向成37o角斜向右上方。
2、 用图象法求合力与分力

 [例4]设有五个力同时作用在质点P,它们的大小和方向相当于正六边形的两条边和三条对角线,如图所示,这五个力中的最小力的大小为F,则这五个力的合力等于( )
[例4]设有五个力同时作用在质点P,它们的大小和方向相当于正六边形的两条边和三条对角线,如图所示,这五个力中的最小力的大小为F,则这五个力的合力等于( )
A、3F B、4F C、5F D、6F
解析:由正六边形的特点可知,当最小的力为F时,最大的力为2F,不难推出F1与F4合力大小为F3,即2F,方向也与F3相同,F2与F5的合力大小为F3,即2F,方向也与F3相同,故最后合力为6F。用力的三角形法则也可得出同样的结论。
2、 按问题的需要进行分解
具体问题的条件有:
①已确定两个分力的大小,可求得分力的方向。
②已确定两个分力的方向,可求得分力的大小。
③已确定一个分力的大小和方向,可求得另上个分力的大小和方向。
④已确定一个分力的大小和另一个分力的方向,可求得一个分力的大小和另一个分力的方向。
力的分解是力的合成的逆运算,同样遵守平行四边形法则,两个分力的合力是唯一确定的,而一个已知力可以分解为大小、方向不同的分力,即一个力的两个分力不是唯一的,要确定一个力的两个分力,应根据具体条件进行。
1、 按力产生的效果进行分解
2、运算法则:
(1)平行四边形法则:求两个互成角度的共点力F1,F2的合力,可以把F1,F2的线段作为邻边作平行四边形,它的对角线即表示合力的大小和方向;
(2)三角形法则:求两个互成角度的共点力F1,F2的合力,可以把F1,F2首尾相接地画出来,把F1,F2的另外两端连接起来,则此连线就表示合力F的大小和方向;
(3)共点的两个力F1,F2的合力F的大小,与它们的夹角θ有关,θ越大,合力越小;θ越小,合力越大,合力可能比分力大,也可能比分力小,F1与F2同向时合力最大,F1与F2反向时合力最小,合力大小的取值范围是 | F1-F2|≤F≤(F1+F2)
(4)三个力或三个以上的力的合力范围在一定的条件下可以是:0≤F≤| F1+F2+…Fn|
1、求几个力的合力叫力的合成,求一个力的分力叫力的分解.
2、合力与它的分力是力的效果上的一种等效替代关系。
1、一个力如果它产生的效果跟几个力共同作用所产生的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力.
5、摩擦力大小的计算与应用
 [例8]如图所示,水平面上两物体 ml、m2经一细绳相连,在水平力F的作用下处于静止状态,则连结两物体绳中的张力可能为(ABC )
[例8]如图所示,水平面上两物体 ml、m2经一细绳相连,在水平力F的作用下处于静止状态,则连结两物体绳中的张力可能为(ABC )
A.零;B.F/2; C.F;D.大于F
解析:当m2与平面间的摩擦力与F平衡时,绳中的张力为零,所以A对;当m2与平面间的最大静摩擦力等于F/2时,则绳中张力为F/2,所以B对,当m2与平面间没有摩擦力时,则绳中张力为F,所以C对,绳中张力不会大于F,因而D错.
答案:ABC
点评:要正确解答该题,必须对静摩擦力,最大静摩擦力有深刻正确的理解.
 [例9]如图所示,传送带与水平面的夹角为370并以10m/s的速度匀速运动着,在传送带的A端轻轻放一小物体,若已知物体与传送带间的动摩擦因数为μ=0.5,AB间距离S=16m,则小物体从A端运动到B端所需的时间为:(1)传送带顺时针方向转动?(2)传送带逆时针方向转动?
[例9]如图所示,传送带与水平面的夹角为370并以10m/s的速度匀速运动着,在传送带的A端轻轻放一小物体,若已知物体与传送带间的动摩擦因数为μ=0.5,AB间距离S=16m,则小物体从A端运动到B端所需的时间为:(1)传送带顺时针方向转动?(2)传送带逆时针方向转动?
A、2.8s;B、2.0s;C、2.1s;D、4.0s;
[分析与解](1)对物体受力分析如图,沿皮带所在的斜面方向有a=gsin370-μgcos370=2m/s2,因物体沿皮带向下运动而皮带向上运动,所以整个过程物体对地匀加速运动16m,据s=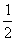 at2得t=4.0s,D选项正确。
at2得t=4.0s,D选项正确。
(2)当物体下滑速度小于传送带时,物体的加速度为a1,(此时滑动摩擦力沿斜面向下)则:a1= =gsin370+μgcos370=10×0.6+0.5×10×0.8=10米/秒2
=gsin370+μgcos370=10×0.6+0.5×10×0.8=10米/秒2
t1=v/a1=10/10=1米,S1=½a1t12=½×10×12=5米
当物体下滑速度大于传送带V=10米/秒 时,物体的加速度为a2(此时f沿斜面向上)则:
a2==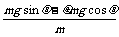 =gsin370-μgcos370=10×0.6-0.5×10×0.8=2米/秒2
=gsin370-μgcos370=10×0.6-0.5×10×0.8=2米/秒2
S2=vt2+½a2t2=(a1t1)t2+½a2t22=10×1×t2+½×2×t22=16-5=11
即:10t2+t22=11 解得:t2=1秒(t2=-11秒舍去)
所以,t=t1+t2=1+1=2秒,B选项正确。
拓展与思考:①皮带不传时与哪种情况类似?
②皮带逆时针转时,若μ=0.8,物体从A到B需多长时间?
③求上述(1)、(2)过程中产生的热量?
注意:在计算摩擦力的大小之前,必须首先分析物体的运动的情况,判明是滑动摩擦,还是静摩擦,若是滑动摩擦,可用 f=μN计算.但要注意N是接触面的正压力,并不总是等于物体的重力。若是静摩擦.一般应根据物体的运动情况(静止、匀速运动或加速运动),利用平衡条件或运动定律求解。 最大静摩擦力(1)大小:fm=μ0N,(2)最大静摩擦力与物体运动趋势无关,而只跟μ0N有关,它比滑动摩擦力略大一些,在许多问题的处理过程中往往将其大小等于滑动摩擦力.
试题展示
 散
力的合成与分解
散
力的合成与分解
基础知识一.合力与分力
4、摩擦力方向的判断与应用
[例7]如图所示,小车的质量为M.人的质量为m,人用恒力 F拉绳,若人和车保持相对静止.不计绳和滑轮质量、车与地面的摩擦,则车对人的摩擦力可能是( )
A、0 ;B、 F,方向向右;C、
F,方向向右;C、 F,方向向左;D
F,方向向左;D F,方向向右
F,方向向右
解析:由于车与人相对静止,则两者加速度相同,即a=2F/(M+m),若车对人的摩擦力向右,人对车的摩擦力向左,则对人:F-f=ma,对车:F+f=Ma,必须M>m。则D正确;若车对人的摩擦力向左,人对车的摩擦力向右,则对人:F+f=ma,对车:F-f=Ma,必须M<m。则C正确;
说明:摩擦力的方向的判定:“摩擦力的方向与物体相对运动或相对运动趋势的方向相反”是判定摩擦力方向的依据,步骤为:①选研究对象(即受摩擦力作用的物体);②选跟研究对象接触的物体为参照物。③找出研究对象相对参照物的速度方向或运动趋势方向.④摩擦力的方向与相对速度或相对运动趋势的方向相反.(假设法判断同样是十分有效的方法)
3、弹簧弹力的计算与应用
[例6]如图,两木块的的质量分别是m1和 m2,两轻弹簧的劲度系数分别为k1和k2,上面的木块压上面的弹簧上,整个系处于平衡状态,现缓慢向上提上面的木块直到它刚离开上面的弹簧,在这个过程中,下面的木块移动的距离为:( C )

解析:对下面的弹簧,初态的弹力为F=(m1+m2)g,末态的弹力为F/=m2g,故Δx=ΔF/k2=m1g/k2。
 说明:研究的弹簧是下面的,劲度系数为k2,力的变化是m1g。
说明:研究的弹簧是下面的,劲度系数为k2,力的变化是m1g。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com