
10.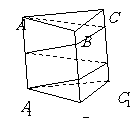 如图,已知正三棱柱
如图,已知正三棱柱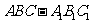 的底面边长为1,高为8,一质点自
的底面边长为1,高为8,一质点自 点出发,沿着三棱柱的侧面绕行两周到达
点出发,沿着三棱柱的侧面绕行两周到达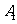 点的最短路线的长为 10.
点的最短路线的长为 10.
考查棱柱、棱锥的概念和性质,以及棱柱、棱锥为载体考查计算能力,想象能力和逻辑推理能力.
要求理解棱柱、直棱柱、正棱柱、平行六面体、长方体及正方体等有关概念,掌握棱柱的性质及长方体对角线性质;理解棱锥、正棱锥的意义,掌握棱锥、正棱锥的性质.
9. 如图,在正三棱柱
如图,在正三棱柱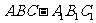 中,
中,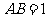 .若二面角
.若二面角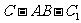 的大小为
的大小为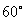 ,则点
,则点 到平面
到平面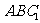 的距离为_____.
的距离为_____. .
.
8.如图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的 中点,则直线AD 与平面B1DC所成角的正弦值为
. 。
。
7.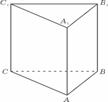 过三棱柱 ABC-A1B1C1 的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有 条.6
过三棱柱 ABC-A1B1C1 的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有 条.6
6.若一条直线与一个正四棱柱各个面所成的角都为 ,则
,则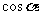 =______
=______
5.在三棱锥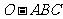 中,三条棱
中,三条棱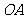 、
、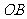 、
、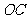 两两互相垂直,且
两两互相垂直,且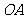 =
=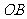 =
=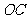 ,
,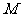 是
是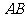 边的中点,则
边的中点,则 与平面
与平面 所成的角的大小是 ( 用反三角函数表示).
所成的角的大小是 ( 用反三角函数表示). 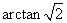 .
.
4.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是 ( B )
A.等腰四棱锥的腰与底面所成的角都相等
B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
C.等腰四棱锥的底面四边形必存在外接圆
D.等腰四棱锥的各顶点必在同一球面上
3.条件M:四棱锥P-ABCD的四个侧面都是全等的等腰三角形,条件N:棱锥P-ABCD是正四棱锥。则M是N的 ( D )
A.充要条件 B.既不充分又不必要条件
C.充分而不必要条件 D.必要而不充分条件
2.设命题甲:“直四棱柱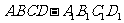 中,平面
中,平面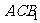 与对角面
与对角面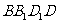 垂直”;命题乙:“直四棱柱
垂直”;命题乙:“直四棱柱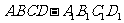 是正方体”,那么,甲是乙的 ( C
)
是正方体”,那么,甲是乙的 ( C
)
A.充分必要条件 B.充分非必要条件
C.必要非充分条件 D.既非充分又非必要条件
1.设M={正四棱柱},N={直四棱柱},P={长方体},Q={直平行六面体},则四个集合的关系为 ( B )
A.M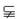 P
P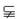 N
N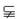 Q
B.M
Q
B.M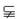 P
P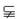 Q
Q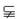 N
N
C.P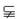 M
M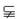 N
N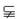 Q D.P
Q D.P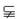 M
M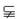 Q
Q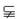 N
N
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com