
17.解:(1)如图,设矩形的另一边长为a m
则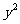 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=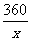 ,
,
所以y=225x+


(II)

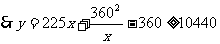 .当且仅当225x=
.当且仅当225x=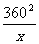 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
17. (本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数: 

(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
16.(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(Ⅰ)确定角C的大小: 

(Ⅱ)若c=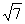 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值。
,求a+b的值。
解(1)由 及正弦定理得,
及正弦定理得,

 是锐角三角形,
是锐角三角形,
(2)解法1: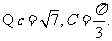 由面积公式得
由面积公式得
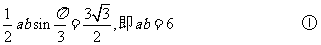
由余弦定理得
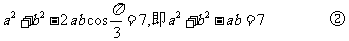
由②变形得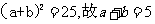
解法2:前同解法1,联立①、②得

消去b并整理得 解得
解得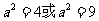
所以 故
故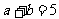
15. 下图是样本容量为200的频率分布直方图。
 根据样本的频率分布直方图估计,样本数据落在[6,10]内的频数为
,数据落在(2,10)内的概率约为
。
根据样本的频率分布直方图估计,样本数据落在[6,10]内的频数为
,数据落在(2,10)内的概率约为
。 

[答案]64
[解析]观察直方图易得频数为 ,频率为
,频率为
14. 过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,则线段PQ的长为 。
[答案]4
[解析]可得圆方程是 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得
13. 设集合A=(x∣log2x<1), B=(X∣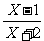 <1), 则A
<1), 则A =
.
=
.
[答案]
[解析]易得A= B=
B=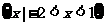 ∴A∩B=
∴A∩B= .
.
12. 甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是 ,三人中至少有一人达标的概率是 。
[答案]0.24 0.76
[解析]三人均达标为0.8×0.6×0.5=0.24,三人中至少有一人达标为1-0.24=0.76
11. 已知(1+ax)3,=1+10x+bx3+…+a3x3,则b=
. 

[答案]40
[解析]因为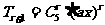 ∴
∴
 .解得
.解得
10.古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如: 


他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数。下列数中及时三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378
[答案]C
[解析]由图形可得三角形数构成的数列通项 ,同理可得正方形数构成的数列通项
,同理可得正方形数构成的数列通项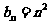 ,则由
,则由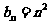
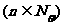 可排除A、D,又由
可排除A、D,又由 知
知 必为奇数,故选C.
必为奇数,故选C.
9.设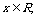 记不超过
记不超过 的最大整数为[
的最大整数为[ ],令{
],令{ }=
}= -[
-[ ],则
],则 {
{ },[
},[ ],
],
A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列
[答案]B
[解析]可分别求得 ,
, .则等比数列性质易得三者构成等比数列.
.则等比数列性质易得三者构成等比数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com