
4.解法一: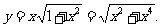 设
设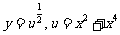 ,则
,则

解法二: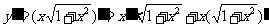

说明:对于复合函数的求导,要注意分析问题的具体特征,灵活恰当地选择中间变量,不可机械照搬某种固定的模式,否则会使确定的复合关系不准确,不能有效地进行求导运算.学生易犯错误是混淆变量或忘记中间变量对自变量求导.
求复合函数的导数
例 求下列函数的导数(其中 是可导函数)
是可导函数)
3.解法一:设 ,则
,则

解法二:

2.解法一:设 ,则
,则
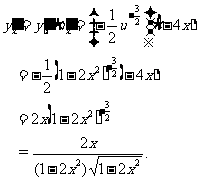
解法二:

3.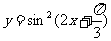 ;4.
;4. 。
。
分析:选择中间变量是复合函数求导的关键.必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的,分清其间的复合关系.要善于把一部分量、式子暂时当作一个整体,这个暂时的整体,就是中间变量.求导时需要记住中间变量,注意逐层求导,不遗漏,而其中特别要注意中间变量的系数.求导数后,要把中间变量转换成自变量的函数.
解:1.解法一:设 ,则
,则

解法二: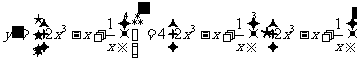

1.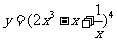 ;2.
;2.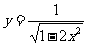 ;
;
4.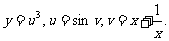
说明:分不清复合函数的复合关系,忽视最外层和中间变量都是基本函数的结构形式,而最内层可以是关于自变量x的基本函数,也可以是关于自变量的基本函数经过有限次的四则运算而得到的函数,导致陷入解题误区,达不到预期的效果.
求函数的导数
例 求下列函数的导数.
3. ;
;
2.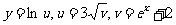 ;
;
1.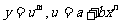 ;
;
3.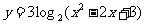 ;4.
;4.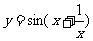 。
。
分析:由复合函数的定义可知,中间变量的选择应是基本函数的结构,解决这类问题的关键是正确分析函数的复合层次,一般是从最外层开始,由外及里,一层一层地分析,把复合函数分解成若干个常见的基本函数,逐步确定复合过程.
解:函数的复合关系分别是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com