12.一天要排语文、数学、英语、生物、体育、班会六节课(上午四节，下午二节)，要求上午第一节不排体育，数学课排在上午，班会课排在下午，问共有多少种不同的排课方法？

解法一:(从数学课排不排第一节入手)

(第一类)数学排在第一节，班会课排在下午，其余四科任排，得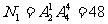

(第二类)数学排在上午另三节中的一节，班会排在下午，体育排在余下(不会第一节)三节中的一节，其余三科任排，得

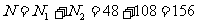　 共有排法(种)

解法二(从体育课入手)

(第一类)体育课在上午　

(第二类)体育课在下午　

　 共有排法(种)

[探索题]三边长均为整数，且最大边长为11的三角形的个数是多少?

解：设较小的两边长为x、y且x≤y，

则 　 x≤y≤11，

x+y>11，

x、y∈N^*.

当x=1时，y=11；

当x=2时，y=10，11；

当x=3时，y=9，10，11；

当x=4时，y=8，9，10，11；

当x=5时，y=7，8，9，10，11；

当x=6时，y=6，7，8，9，10，11；

当x=7时，y=7，8，9，10，11；

……

当x=11时，y=11.

所以不同三角形的个数为

1+2+3+4+5+6+5+4+3+2+1=36.

评述：本题关键是列出约束条件，然后寻找x=1，2，…，11时，y的取值个数的规律，再用分类计数原理求解.

11.用1，2，3，4，5排成一个数字不重复的五位数a₁a₂a₃a₄a₅，满足a₁<a₂，a₂>a₃，a₃<a₄，a₄>a₅的五位数有多少个？

解：因为a₂>a₁、a₃，a₄>a₃、a₅，所以a₂只能是3、4、5.

(1)若a₂=3，则a₄=5，a₅=4，a₁与a₃是1或2，这时共有A=2个符合条件的五位数.

(2)若a₂=4，则a₄=5，a₁、a₃、a₅可以是1、2、3，共有A=6个符合条件的五位数.

(3)若a₂=5，则a₄=3或4，此时分别与(1)(2)情况相同.

所以，满足条件的五位数有2(A+A)=16个.