
2、水的性质
物理性质:无色无味的液体、40C时密度最大,为1g/cm3
化学性质:通电分解
文字表达式:水(H2O) 氢气(H2) + 氧气(O2)
氢气(H2) + 氧气(O2)
化学方程式: 2H2O  2H2↑+O2↑
2H2↑+O2↑
1、水的组成:(考点一)
(1)电解水的实验
A.装置―――水电解器
B.电源种类---直流电
C.加入硫酸或氢氧化钠的目的----增强水的导电性
D.化学反应:文字表达式::水(H2O) 氢气(H2) + 氧气(O2)
氢气(H2) + 氧气(O2)
|
 2H2↑+ O2↑
2H2↑+ O2↑
产生位置 负极 正极
体积比 2 : 1
质量比 1 : 8
E.检验:O2---出气口置一根带火星的木条----木条复燃
H2---出气口置一根燃着的木条------气体燃烧,发出淡蓝色的火焰
(2)结论: ①水是由氢、氧元素组成的。
②化学变化中,分子可分而原子不可分。
20. 已知函数
已知函数
 上恒成立
上恒成立
(1)求 的值;
的值;
(2)若
(3)是否存在实数m,使函数 上有最小值-5?若
上有最小值-5?若
存在,请求出实数m的值;若不存在,请说明理由.
解:(1)

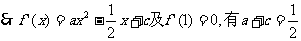
 恒成立
恒成立
即 恒成立
恒成立
显然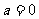 时,上式不能恒成立
时,上式不能恒成立
 是二次函数
是二次函数
由于对一切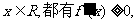 于是由二次函数的性质可得
于是由二次函数的性质可得
 即
即
 .
.
(2)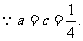


即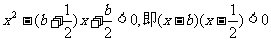
当 ,当
,当 .
.
(3)

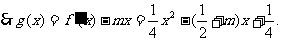
该函数图象开口向上,且对称轴为
假设存在实数m使函数 区间
区间 上有
上有
最小值-5.
①当 上是递增的.
上是递增的.

解得

 舍去
舍去
②当 上是递减的,而在
上是递减的,而在
区间 上是递增的,
上是递增的,

即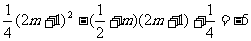
解得
③当 时,
时, 上递减的
上递减的

即
解得 应舍去.
应舍去.
综上可得,当 时,
时,
函数
19.数列{an}满足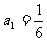 ,前n项和
,前n项和 ,
,
(1)写出
(2)猜出 ,并用数学归纳法证明。
,并用数学归纳法证明。
解:(1)由 得:
得:
由 得:
得:
由 得:
得:
(2)猜想:
证明:①当n=1时,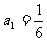 ,
, ,等式成立。
,等式成立。
②假设当n=k时等式成立,则 ,当n=k+1时,
,当n=k+1时,




 ,综合①②,等式成立。
,综合①②,等式成立。
17.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为 ,记
,记 .
.
(1)分别求出 取得最大值和最小值时的概率;
取得最大值和最小值时的概率;
(2)求 的分布列及数学期望.
的分布列及数学期望.
解:(1)掷出点数 可能是:
可能是:
则 分别得:
分别得: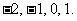 于是
于是 的所有取值分别为:
的所有取值分别为:
因此 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
当 且
且 时,
时, 可取得最大值
可取得最大值 ,
,
此时, ;
;
当 且
且 时,
时, 可取得最小值
可取得最小值 .
.
此时, .
.
(2)由(Ⅰ)知 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
 ;
;
当 =1时,
=1时,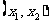 的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即 ;
;
当 =2时,
=2时,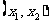 的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
即 ;
;
当 =4时,
=4时,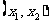 的所有取值为(1,3)、(3,1).即
的所有取值为(1,3)、(3,1).即 ;
;
当 =5时,
=5时,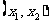 的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即 .
.
所以ξ的分布列为:
|
ξ |
0 |
1 |
2 |
4 |
5 |
8 |
|
P |
 |
 |
 |
 |
 |
 |
18
已知函数 .
.
(Ⅰ)若函数 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点
 ,
,
 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(Ⅱ)若 ,试讨论函数
,试讨论函数 的单调性.
的单调性.
解:(Ⅰ)函数 的定义域为
的定义域为 .
.
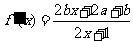
由题意 ,解得
,解得
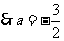 .
.
(Ⅱ)若 , 则
, 则 .
.
 .
.
(1)令 ,由函数定义域可知,
,由函数定义域可知, ,所以
,所以
①当 时,
时, ,
, ,函数
,函数 单调递增;
单调递增;
②当 时,
时, ,
, ,函数
,函数 单调递增;
单调递增;
(2)令 ,即
,即
①当 时,不等式
时,不等式 无解;
无解;
②当 时,
时,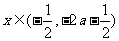 ,
, ,函数
,函数 单调递减;
单调递减;
综上:当 时,函数
时,函数 在区间
在区间 为增函数;
为增函数;
当 时,函数
时,函数 在区间
在区间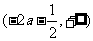 为增函数;
为增函数;
在区间 为减函数.
为减函数.
16. 在三棱锥
在三棱锥 中,
中, 和
和 是边长为
是边长为 的等边三角形,
的等边三角形, ,
,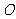 是
是 中点.
中点.
(Ⅰ)在棱 上求一点
上求一点 ,使得
,使得 ∥平面
∥平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角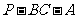 的余弦值.
的余弦值.
解
(Ⅰ)当 为棱
为棱 中点时,
中点时, ∥平面
∥平面 .
.
证明如下:
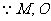 分别为
分别为 中点,
中点,

 ∥
∥
又 平面
平面 ,
, 平面
平面
 ∥平面
∥平面 .
.
(Ⅱ)连结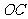 ,
,
 ,
,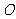 为
为 中点,
中点, ,
,
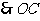 ⊥
⊥ ,
, .
.
同理,  ⊥
⊥ ,
,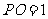 .
.
 又
又 ,
,
 ,
,
 .
.
 ⊥
⊥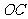 .
.

 ⊥
⊥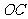 ,
, ⊥
⊥ ,
, ,
,
 ⊥平面
⊥平面 .
.
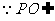 平面
平面
 平面
平面 ⊥平面
⊥平面 .
.
(Ⅲ)如图,建立空间直角坐标系 .
.
则 ,
,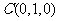 ,
, ,
,
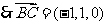 ,
, .
.
由(Ⅱ)知 是平面
是平面
的一个法向量.
设平面 的法向量为
的法向量为 ,
,
则 .
.
令 ,则
,则 ,
,
 平面
平面 的一个法向量
的一个法向量 .
.
 .
.
 二面角
二面角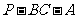 的平面角为锐角,
的平面角为锐角,
 所求二面角
所求二面角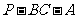 的余弦值为
的余弦值为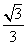 .
.
15. 已知A,B,C为锐角 的三个内角,向量
的三个内角,向量 ,
,
 ,且
,且 .
.
(Ⅰ)求A的大小;(Ⅱ)求 取最大值时角B的大小.
取最大值时角B的大小.
解:(Ⅰ)
 ,
,


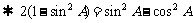
 .
.
 是锐角三角形,
是锐角三角形, .
.
(Ⅱ) 是锐角三角形,且
是锐角三角形,且 ,
, 



当 取最大值时,
取最大值时, 即
即 .
.
14.若满足 的实数
的实数 ,使不等式
,使不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是

13. 观察以下不等式:


……
可以归纳出对于大于1的正整数n成立的一个不等式 ,则右端f(n)的表达式应该为
,则右端f(n)的表达式应该为 。
。
12. 直线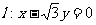 与曲线
与曲线 (
( 为参数,
为参数, )有两个公共点
)有两个公共点 ,且
,且 ,则实数
,则实数 的值为 2 ;在此条件下,以直角坐标系的原点为极点,
的值为 2 ;在此条件下,以直角坐标系的原点为极点, 轴正方向为极轴建立极坐标系,则曲线
轴正方向为极轴建立极坐标系,则曲线 的极坐标方程为
的极坐标方程为 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com