
9.(2006重庆)已知函数f(x)=(x2+bx+c)ex,其中b,c∈R为常数。
(Ⅰ)若b2>4(c-1),讨论函数f(x)的单调性;
(Ⅱ)若 ,且
,且 ,试证:
,试证: 。
。
解(I)求导得f/(x)=[x2+(b+2)x+b+e]ex
∵b2>4(c-1)故方程f/(x)=0 即 x2+(b+2)x+b+e=0有两个实根

令f/(x)>0,解得x<x1,或x>x2.
又令f/(x)<0,解得x1<x<x2.
故当x∈(-∞,x1)时,f(x)是增函数,x∈(x2,+∞)时,f(x)也是函数,当x∈(x1,x2)时,f(x)是减函数。
(II)易知
∴
∴由已知条件得
解得
8.(2006江西)已知函数 在
在 与
与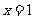 时都取得极值.
时都取得极值.
(1)求 、
、 的值及函数f(x)的单调区间;
的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
解: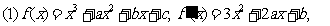

f/(x)=3x2-x-2=(3x-2)(x-1),函数f(x)的单调区间如下表:
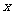 |
 |
 |
 |
 |
 |
|
f/(x) |
 |
 |
 |
 |
 |
|
f(x) |
 |
极大值 |
 |
极小值 |
 |
所以函数f(x)的递增区间为 与
与 ;
;
递减区间为 .
.

7. 已知x∈R,求证:ex≥x+1.
证明:设f(x)=ex-x-1,则f′(x)=ex-1.
∴当x=0时,f′(x)=0,f(x)=0.
当x>0时,f′(x)>0,∴f(x)在(0,+∞)上是增函数.∴f(x)>f(0)=0.
当x<0时,f′(x)<0,f(x)在(-∞,0)上是减函数,∴f(x)>f(0)=0.
∴对x∈R都有f(x)≥0.∴ex≥x+1.
5.  ; 6.设底面边长为x,则高为h=
; 6.设底面边长为x,则高为h= ,
,
∴S表=3× x+2×
x+2×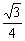 x2=
x2= +
+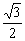 x2
x2
∴S′=- +
+ x
x 令S′=0,得x=
令S′=0,得x= .答案:
.答案: 
[解答题]
4. ,
,
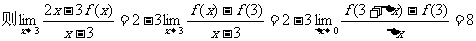
3.由f(-x)=f(x),求导得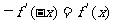 .
.
2. (x)=4x(x2-3x+5)在[1,2]上,
(x)=4x(x2-3x+5)在[1,2]上, (x)>0,
(x)>0,
∴f(x)在[1,2]上单调递增.∴f(x)≥f(1)=7.
∴f(x)=0在[1,2]上无根.答案:D
5.曲线y= 上的点到直线2x-y+3=0的最短距离为
上的点到直线2x-y+3=0的最短距离为
6 设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为________
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为________
简答.提示:1-4.DDBC;
4.已知 的值是 ( )
的值是 ( )
A. B.0 C.8 D.不存在
B.0 C.8 D.不存在
[填空题]
3.若f(x)是在(-L,L)内的可导的偶函数,且 不恒为0,则
不恒为0,则 ( )
( )
(A)必定是(-L,L)内的偶函数
(B)必定是(-L,L)内的奇函数
(C)必定是(-L,L)内的非奇非偶函数
(D)可能是(-L,L)内的奇函数,可能是偶函
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com