
4.与向量
 的夹解相等,且模为1的向量是
的夹解相等,且模为1的向量是
A.  B.
B.  或
或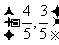
C. D.
D. 或
或
3.已知点 ,
, ,
, ,
,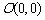 .给出下面的结论:①
.给出下面的结论:①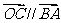 ;②
;②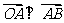 ;③
;③ ;④
;④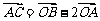 . 其中正确结论的个数是
. 其中正确结论的个数是
A. 4个 B.3个 C.2个 D.1个
2.已知向量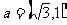 ,
,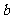 是不平行于
是不平行于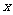 轴的单位向量,且
轴的单位向量,且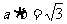 ,则
,则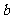 =
=
A. 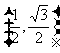 B.
B.
 C.
C.  D.
D. 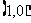
1.P是△ABC所在平面上一点,若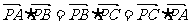 ,则P是△ABC的
,则P是△ABC的
A 外心 B 内心 C 重心 D 垂心
5.某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元、2000元。甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工1件甲设备所需工时分别为 ,加工1件乙设备所需工时分别为,A、B两种设备每月有效使用台时数分别为
,加工1件乙设备所需工时分别为,A、B两种设备每月有效使用台时数分别为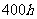 和
和 。如何安排生产可使收入最大?
。如何安排生产可使收入最大?
4.若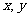 满足条件
满足条件 ,求目标函数
,求目标函数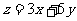 的最小值。
的最小值。
3.若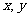 满足条件
满足条件 ,求
,求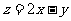 的最大值。
的最大值。
2.已知实数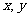 满足线性约束条件
满足线性约束条件 ,那么它的可行域的面积是 。若目标函数为
,那么它的可行域的面积是 。若目标函数为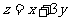 ,则目标函数的最大值为 ,此时的最优解为
;若目标函数为
,则目标函数的最大值为 ,此时的最优解为
;若目标函数为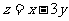 ,则目标函数的最小值为 ,此时的最优解为
。
,则目标函数的最小值为 ,此时的最优解为
。
1.在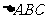 中,三顶点分别为
中,三顶点分别为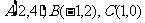 点
点 在
在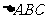 的内部及其边界上运动,则
的内部及其边界上运动,则 的取值范围为(
)
的取值范围为(
)
A. B.
B.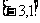 C.
C. 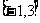 D.
D.
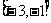
2、初步掌握简单线性规划问题解决实际问题的方法;
重点:用图解法求线性目标函数的最值问题。
难点:①生活问题数学化(数学建模);②用图解法求线性目标函数的最值问题。
教 学 过 程 设 计
|
 活动1:画出不等式组
活动1:画出不等式组
|
|
 在现实生产、生活中,经常会遇到资源利用、人力调配、生产安排等问题,下面我们来看一个具体的实例。
在现实生产、生活中,经常会遇到资源利用、人力调配、生产安排等问题,下面我们来看一个具体的实例。
活动2:某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时 ,每生产一件乙产品使用4个B配件并耗时
,每生产一件乙产品使用4个B配件并耗时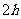 ,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8
,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8 计算。
计算。
问题1:设甲、乙两种产品分别生产 、
、 件,请列表分析并用数学关系表示上述问题的要求(即生活问题数学化)。
件,请列表分析并用数学关系表示上述问题的要求(即生活问题数学化)。
问题2:用平面区域表示上述数学关系。
|

|
|
该厂应怎样安排每天的生产任务才是合理的?
活动3:(接活动2)若已知该厂生产一件甲产品获利2万元,生产一件乙产品获利3万元。设甲、乙两种产品分别生产 、
、 件,请用数学关系表示该厂的利润
件,请用数学关系表示该厂的利润 ,并说明这个表示什么几何意义。
,并说明这个表示什么几何意义。
活动4:(接活动3)请问厂家应该怎样安排生产,才能使利润 达到最大,
达到最大,
并求出这个最大值?
活动5:请同学们预习课本 第2段,并完成下面的问题。
第2段,并完成下面的问题。
问题1:什么叫线性约束条件?上述问题的线性约束条件是____________________________
问题2:什么叫目标函数、线性目标函数?上述问题的线性目标函数是__________________
问题3:什么叫线性规划?上述问题是否一个线性规划________________________________
问题4:什么叫可行解?上述问题的可行解是________________________________________
问题5:什么叫可行域?上述问题的可行域是________________________________________
问题6:什么叫最优解?上述问题的最优解是________________________________________
活动6:某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时 ,每生产一件乙产品使用4个B配件并耗时
,每生产一件乙产品使用4个B配件并耗时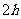 ,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8
,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8 计算。若已知该厂生产一件甲产品获利3万元,生产一件乙产品获利2万元,请问应当如何安排生产才能获得最大利润,并求出最大利润。
计算。若已知该厂生产一件甲产品获利3万元,生产一件乙产品获利2万元,请问应当如何安排生产才能获得最大利润,并求出最大利润。
活动7:请根据以上的求解过程归纳出利用图解决线性规划问题的一般步骤。
课后练习:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com