
1.在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF、GH交于一点P,则 ( B )
A.P点一定在直线BD上
B.P点一定在直线AC上
C.P点在直线AC和BD上
D.P点既不在直线BD上,也不在直线AC上
|
|
内容 |
要求 |
||
|
A |
B |
C |
||
|
1 |
平面及其基本性质 |
|
√ |
|
|
2 |
几何体的直观图 |
√ |
|
|
|
3 |
异面直线所成的角 |
|
√ |
|
|
4 |
异面直线的距离(给出异面直线的公垂线) |
√ |
|
|
|
5 |
直线和平面平行的判定与性质 |
|
√ |
|
|
6 |
直线和平面垂直的判定与性质 |
|
|
√ |
|
7 |
斜线在平面上的射影、直线与平面所成的角 |
|
√ |
|
|
8 |
点到平面的距离、直线和平面的距离 |
|
√ |
|
|
9 |
三垂线定理及其逆定理 |
|
√ |
|
|
10 |
平面平行的判定与性质 |
|
√ |
|
|
11 |
两平行平面间的距离 |
|
√ |
|
|
12 |
二面角、二面角的平面角 |
|
√ |
|
|
13 |
两个平面垂直的判定与性质 |
|
√ |
|
22.已知向量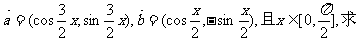
(1) ;
;
(2)(理科做)若
(文科做)求函数 的最小值。
的最小值。
21.已知点A、B、C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),α (
(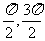 )。
)。
(1)若 ,求角α的值;
(2)若
,求角α的值;
(2)若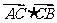 =-1,求
=-1,求 的值.
的值.
20.在平面直角坐标系中,已知 ,满足向量
,满足向量 与向量
与向量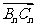 共线,且点
共线,且点 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若 。求
。求
(1)数列 的通项
的通项 (2)数列{
(2)数列{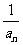 }的前n项和
}的前n项和
19.已知M=(1+cos2x,1),N=(1,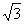 sin2x+a)(x,a∈R,a是常数),且y =
sin2x+a)(x,a∈R,a是常数),且y = ·
· (O是坐标原点)(1)求y关于x的函数关系式y=f(x);
(O是坐标原点)(1)求y关于x的函数关系式y=f(x);
(2)若x∈[0, ],f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由y=2sin(x+
],f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由y=2sin(x+ )的图象经过怎样的变换而得到.
)的图象经过怎样的变换而得到.
18.设向量 ,向量
,向量 垂直于向量
垂直于向量 ,向量
,向量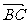 平行于
平行于 ,试求
,试求 的坐标.
的坐标.
17.已知△ABC中,∠C=120°,c=7,a+b=8,求 的值。
的值。
16.下列命题中:
① ∥
∥
 存在唯一的实数
存在唯一的实数 ,使得
,使得 ;
;
② 为单位向量,且
为单位向量,且 ∥
∥ ,则
,则 =±|
=±| |·
|· ;③
;③ ;
;
④ 与
与 共线,
共线, 与
与 共线,则
共线,则 与
与 共线;⑤若
共线;⑤若
其中正确命题的序号是 .
15.已知点A(2,0),B(4,0),动点P在抛物线y2=-4x运动,则使 取得最小值的点P的坐标是
.
取得最小值的点P的坐标是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com