
4.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若 ;
;
②若m、l是异面直线, ;
;
③若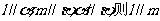 ;
;
④若
其中为假命题的是 ( C )
A.① B.② C.③ D.④
3.已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是 ( D )
A.平面ABC必平行于α
B.平面ABC必与α相交
C.平面ABC必不垂直于α
D.存在△ABC的一条中位线平行于α或在α内
2.平面α⊥β,α∩β=a,点P∈α,Q∈a,那么PQ⊥a是PQ⊥β的 ( C )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
其中真命题的个数是 ( B )
A.4 B.3 C.2 D.1
6. 如图,在五面体
如图,在五面体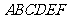 中,点
中,点 是矩形
是矩形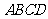 的对角线的交点,面
的对角线的交点,面 是等边三角形,棱
是等边三角形,棱 .
.
(1)证明 //平面
//平面 ;
;
(2)设 ,证明
,证明 平面
平面 .
.
解:(1)证明:取CD中点M,连结OM.
在矩形ABCD中, ,
,
又 ,则
,则 ,
,
连结EM,于是四边形EFOM为平行四边形. ,
,
又 平面CDE,EM
平面CDE,EM 平面CDE,
平面CDE,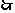 FO∥平面CDE
FO∥平面CDE
(2)证明:连结FM,由(1)和已知条件,
在等边△CDE中, 且
且 .
.
因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,∴CD⊥平面EOM,
从而CD⊥EO.而 ,所以EO⊥平面CDF.
,所以EO⊥平面CDF.
考查直线与平面位置关系.要求掌握直线与平面平行、垂直的判定定理和性质定理.会运用 “转化”的方法判定直线和平面平行与垂直.
5. 是空间两条不同直线,
是空间两条不同直线, 是两个不同平面,下面有四个命题:
是两个不同平面,下面有四个命题:
① ②
②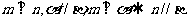
③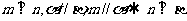 ④
④
其中真命题的编号是 ;(写出所有真命题的编号)①、④.
4.已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是:
①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.
在上面结论中,正确结论的编号是__________.①②④(写出所有正确结论的编号)
3.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有 ( D )
A.4条 B.6条 C.8条 D.12条
2.设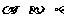 为平面,
为平面, 为直线,则
为直线,则 的一个充分条件是 ( D
)
的一个充分条件是 ( D
)
A. B.
B.
C. D.
D.
1.对于平面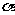 和共面的直线m、n,下列命题中真命题是
( C
)
和共面的直线m、n,下列命题中真命题是
( C
)
A.若m⊥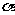 ,m⊥n,则n∥
,m⊥n,则n∥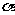 B.若m∥
B.若m∥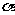 ,n∥
,n∥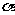 ,则m∥n
,则m∥n
C.若m
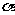 ,n∥
,n∥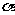 ,则m∥n D.若m、n与
,则m∥n D.若m、n与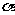 所成的角相等,则n∥m
所成的角相等,则n∥m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com