
12. 如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边∆ AB1C所在的平面与底面ABC垂直,且
如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边∆ AB1C所在的平面与底面ABC垂直,且 ACB=90°,设AC=2a,BC=a.
ACB=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(1)证明:∵平面 ∥平面
∥平面 ,
,
 ,
,


又∵平面 ⊥平面
⊥平面 ,平面
,平面 ∩平面
∩平面 ,
,
∴ ⊥平面
⊥平面 ,
,
 ,
,
又 ,
, .
. 为
为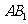 与
与 的公垂线.
的公垂线.
(2)解法1:过A作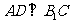 于D, ∵△
于D, ∵△ 为正三角形,∴D为
为正三角形,∴D为 的中点.
的中点.
∵BC⊥平面 ∴
∴ ,
,
又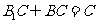 ,∴AD⊥平面
,∴AD⊥平面 ,
,
∴线段AD的长即为点A到平面 的距离.
的距离.
在正△ 中,
中, .
.
∴点A到平面 的距离为
的距离为 .
.
解法2:取AC中点O连结 ,则
,则 ⊥平面
⊥平面 ,且
,且 =
= .
.
由(1)知 ,设A到平面
,设A到平面 的距离为x,
的距离为x, ,
,
即 ,解得
,解得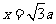 .
.
即A到平面 的距离为
的距离为 .
.
所以 到平面
到平面 的距离为
的距离为 .
.
空间的距离有:点与点、点到直线、点到平面、两平行直线、两异面直线、线与面、面与面、球面上两点间的距离。这七种距离一般都可以转化为点到点、点到线、点到面这三种距离,其中,点到面的距离是重点.
在求距离的过程中,常常由“作出距离”、“证明”、“计算”三部分组成。
在计算点到面的距离时,常将所求的“垂线段”放到某一个平面中加以分析,运用勾股定理、正余弦定理进行计算, 或运用等积法进行计算。
11.已知l是过正方体ABCD-A1B1C1D1的顶点的平面AB1D1与下底面ABCD所在平面的交线,
(1)求证:D1B1∥l;
(2)若AB=a,求l与D1间的距离.
(1)证明:∵D1B1∥BD,∴D1B1∥平面ABCD.
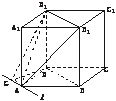
又平面ABCD∩平面AD1B1=l,∴D1B1∥l.
(2)解:∵D1D⊥平面ABCD,
在平面ABCD内,由D作DG⊥l于G,连结D1G,
则D1G⊥l,D1G的长即等于点D1与l间的距离.
∵l∥D1B1∥BD,∴∠DAG=45°.
∴DG=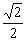 a,D1G=
a,D1G= =
= =
= a.
a.
10.在空间四边形ABCD中,AD=AC=BD=BC=a,AB=CD=b,E、F分别是AB、CD的中点.
(1)求证:EF是AB和CD的公垂线;
(2)求AB和CD间的距离.
证明:(1)连结AF、BF,
 ,∴
,∴ ,
,
∴ .又
.又 ,∴
,∴ ,同理:EF
,同理:EF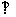 CD.
CD.
∴EF是AB和CD的公垂线.
解:(2)EF就是AB和CD的距离.在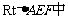 ,
,






9.已知Rt△ABC的直角顶点C在平面α内,斜边AB∥α,AB=2 ,AC、BC分别和平面α成45°和30°角,则AB到平面α的距离为__________.2
,AC、BC分别和平面α成45°和30°角,则AB到平面α的距离为__________.2

8.如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是 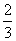 .
.
7.在 中,
中, ,
, 所在平面外一点
所在平面外一点 到三顶点
到三顶点 的距离都是
的距离都是 ,则
,则 到平面
到平面 的距离是
(
的距离是
( 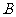 )
)

A. B.
B.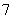 C.
C. D.
D.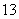
6.把边长为 的正三角形
的正三角形 沿高线
沿高线 折成
折成 的二面角,点
的二面角,点 到
到 的距离是( D)
的距离是( D)
A. B.
B.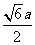 C.
C. D.
D.
5.在四面体 中,
中, 两两垂直,
两两垂直,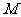 是面
是面 内一点,
内一点,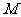 到三个面
到三个面 的距离分别是
的距离分别是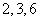 ,则
,则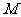 到
到 的距离是 (
的距离是 (  )
)
A.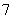 B.
B.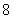 C.
C. D.
D.
4.已知 正方形
正方形 所在平面,
所在平面,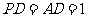 ,点
,点 到平面
到平面 的距离为
的距离为 ,点
,点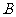 到平面
到平面 的距离为
的距离为 ,则
( D )
,则
( D )
A. B.
B. C.
C.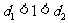 D.
D.
3.正方体ABCD-A1B1C1D1的棱长为1,E是A1B1的中点,则E到平面AB C1D1的距离为 ( B )
A. B.
B. C.
C. D.
D.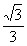
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com