5.随机数表法： 随机数表抽样“三步曲”：第一步，将总体中的个体编号；第二步，选定开始的数字；第三步，获取样本号码

4.抽签法：先将总体中的所有个体(共有N个)编号(号码可从1到N)，并把号码写在形状、大小相同的号签上(号签可用小球、卡片、纸条等制作)，然后将这些号签放在同一个箱子里，进行均匀搅拌，抽签时每次从中抽一个号签，连续抽取n次，就得到一个容量为n的样本

适用范围：总体的个体数不多时

优点：抽签法简便易行，当总体的个体数不太多时适宜采用抽签法．

3.⑴用简单随机抽样从含有N个个体的总体中抽取一个容量为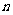的样本时，每次抽取一个个体时任一个体被抽到的概率为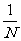；在整个抽样过程中各个个体被抽到的概率为；

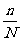　　 ⑵简单随机抽样的特点是，逐个抽取，且各个个体被抽到的概率相等；

　　 ⑶简单随机抽样方法，体现了抽样的客观性与公平性，是其他更复杂抽样方法的基础．

2.简单随机抽样：设一个总体的个体数为N．如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样

1. 在统计学里，我们把所要考察对象的全体叫做总体，其中的每一个考察对象叫做个体，从总体中所抽取的一部分个体叫做总体的一个样本，样本中个体的数目叫做样本的容量．总体中所有个体的平均数叫做总体平均数，样本中所有个体的平均数叫做样本平均数．

3．在△ABC中，已知cos(+A)＝，则cos2A的值为________．

解析：cos(+A)＝coscosA－sinsinA

＝(cosA－sinA)＝，

∴cosA－sinA＝＞0.　　　　　　　　　　　　　　　　　　　　　　　　 ①

∴0＜A＜，∴0＜2A＜

①²得1－sin2A＝，∴sin2A＝.

∴cos2A＝＝.

2．(2010·平顶山模拟)在△ABC中，sin²A+cos²B＝1，则cosA+cosB+cosC的最大值为(　)

A.　 　　　B.　　　　 C．1 　　　　D.

解析：由sin²A+cos²B＝1，得sin²A＝sin²B，

∴A＝B，故cosA+cosB+cosC＝2cosA－cos2A

＝－cos²A+2cosA+1.

又0＜A＜，0＜cosA＜1.

∴cosA＝时，有最大值.

答案：D

1.如果α∈(，π)，且sinα＝，那么sin(α+)+cos(α+)＝　　　　　　　　　　 (　)

A.　 　　B．－　　　 C.　 　　D．－

解析：∵sinα＝，＜α＜π，∴cosα＝－，而sin(α+)+cos(α+)＝sin(α+)＝　　

cosα＝－.

答案：D

4．两个平面垂直的性质.

3．应用两个平面垂直的判定定理的关键是将面面垂直的问题转化为线面垂直的问题；