
31、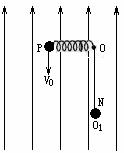 (2009年四川卷)25.如图所示,轻弹簧一端连于固定点O,可在竖直平面内自由转动,另一端连接一带电小球P,其质量m=2×10-2 kg,电荷量q=0.2 C。将弹簧拉至水平后,以初速度V0=20 m/s竖直向下射出小球P,小球P到达O点的正下方O1点时速度恰好水平,其大小V=15 m/s。.若O、O1相距R=1.5 m,小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场。此后,小球P在竖直平面内做半径r=0.5 m的圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取g=10 m/s2。那么,
(2009年四川卷)25.如图所示,轻弹簧一端连于固定点O,可在竖直平面内自由转动,另一端连接一带电小球P,其质量m=2×10-2 kg,电荷量q=0.2 C。将弹簧拉至水平后,以初速度V0=20 m/s竖直向下射出小球P,小球P到达O点的正下方O1点时速度恰好水平,其大小V=15 m/s。.若O、O1相距R=1.5 m,小球P在O1点与另一由细绳悬挂的、不带电的、质量M=1.6×10-1 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=1T的弱强磁场。此后,小球P在竖直平面内做半径r=0.5 m的圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取g=10 m/s2。那么,
(1)弹簧从水平摆至竖直位置的过程中,其弹力做功为多少?
(2)请通过计算并比较相关物理量,判断小球P、N碰撞后能否在某一时刻具有相同的速度。
(3)若题中各量为变量,在保证小球P、N碰撞后某一时刻具有相同速度的前提下,请推导出r的表达式(要求用B、q、m、θ表示,其中θ为小球N的运动速度与水平方向的夹角)。
[解析](1)设弹簧的弹力做功为W,有:
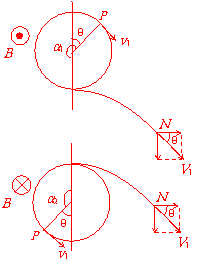

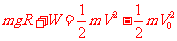 ①
①
代入数据,得:W= J ②
J ②
(2)由题给条件知,N碰后作平抛运动,P所受电场力和重力平衡,P带正电荷。设P、N碰后的速度大小分别为v1和V,并令水平向右为正方向,有:  ③
③
而: 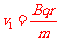 ④
④
若P、N碰后速度同向时,计算可得V<v1,这种碰撞不能实现。P、N碰后瞬时必为反向运动。有:  ⑤
⑤
P、N速度相同时,N经过的时间为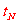 ,P经过的时间为
,P经过的时间为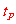 。设此时N的速度V1的方向与水平方向的夹角为
。设此时N的速度V1的方向与水平方向的夹角为 ,有:
,有:
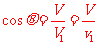 ⑥
⑥
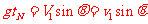 ⑦
⑦
代入数据,得: 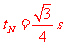 ⑧
⑧
对小球P,其圆周运动的周期为T,有:
 ⑨
⑨
经计算得: 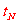 <T,
<T,
P经过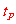 时,对应的圆心角为
时,对应的圆心角为 ,有:
,有: 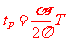 ⑩
⑩
当B的方向垂直纸面朝外时,P、N的速度相同,如图可知,有: 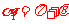
联立相关方程得: 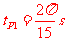
比较得, 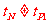 ,在此情况下,P、N的速度在同一时刻不可能相同。
,在此情况下,P、N的速度在同一时刻不可能相同。
当B的方向垂直纸面朝里时,P、N的速度相同,同样由图,有: 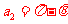 ,
,
同上得:  ,
,
比较得,  ,在此情况下,P、N的速度在同一时刻也不可能相同。
,在此情况下,P、N的速度在同一时刻也不可能相同。
(3)当B的方向垂直纸面朝外时,设在t时刻P、N的速度相同, 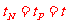 ,
,
再联立④⑦⑨⑩解得: 
当B的方向垂直纸面朝里时,设在t时刻P、N的速度相同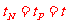 ,
,
同理得:  ,
,
考虑圆周运动的周期性,有: 
(给定的B、q、r、m、 等物理量决定n的取值)
等物理量决定n的取值)
30、(2009年浙江卷)24.某校物理兴趣小组决定举行遥控塞车比赛。比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,出B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟。已知赛车质量m=0.1kg,通电后以额定功率ρ=1.5W工作,进入竖直圆轨道前受到的阻值为0.3N,随后在运动中受到的阻力均可不计。图中L=10.00m,R=0.32m,h=1.25m,S=1.50m。问:要使赛车完成比赛,电动机至少工作多长时间?(取g=10 m/s2)

 答案2.53s
答案2.53s
 [解析]
[解析]  设赛车越过壕沟需要的最小速度为v1,由平抛运动的规律
设赛车越过壕沟需要的最小速度为v1,由平抛运动的规律

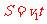

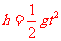
 解得
解得
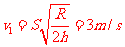
 设赛车恰好越过圆轨道,对应圆轨道最高点的速度为v2,最低点的速度为v3,由牛顿第二定律及机械能守恒定律
设赛车恰好越过圆轨道,对应圆轨道最高点的速度为v2,最低点的速度为v3,由牛顿第二定律及机械能守恒定律



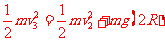
 解得
解得  m/s
m/s
 通过分析比较,赛车要完成比赛,在进入圆轨道前的速度最小应该是
通过分析比较,赛车要完成比赛,在进入圆轨道前的速度最小应该是

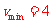 m/s
m/s
 设电动机工作时间至少为t,根据功能原理
设电动机工作时间至少为t,根据功能原理

 由此可得
t=2.53s
由此可得
t=2.53s
29、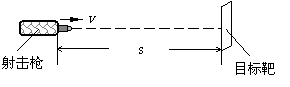 (2009年福建卷)20.
(2009年福建卷)20. 如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100 m,子弹射出的水平速度v=200m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10 m/s2,求:
如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100 m,子弹射出的水平速度v=200m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10 m/s2,求:
 (1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶?
(1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶?
 (2)目标靶由静止开始释放到被子弹击中,下落的距离h为多少?
(2)目标靶由静止开始释放到被子弹击中,下落的距离h为多少?
 答案(1)0.5s(2)1.25m
答案(1)0.5s(2)1.25m
[解析](1)子弹做平抛运动,它在水平方向的分运动是匀速直线运动,设子弹经t时间集中目标靶,则
 t=
t=
 代入数据得
代入数据得
 t=0.5s
t=0.5s
 (2)目标靶做自由落体运动,则h=
(2)目标靶做自由落体运动,则h=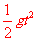
 代入数据得 h=1.25m
代入数据得 h=1.25m
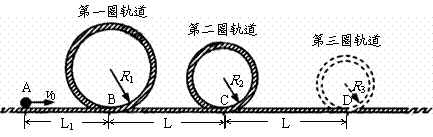
28、(2009年安徽卷)24.过山车是游乐场中常见的设施。下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径R1=2.0m、R2=1.4m。一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以v0=12.0m/s的初速度沿轨道向右运动,A、B间距L1=6.0m。小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。重力加速度取g=10m/s2,计算结果保留小数点后一位数字。试求
(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小;
(2)如果小球恰能通过第二圆形轨道,B、C间距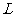 应是多少;
应是多少;
(3)在满足(2)的条件下,如果要使小球不能脱离轨道,在第三个圆形轨道的设计中,半径R3应满足的条件;小球最终停留点与起点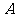 的距离。
的距离。

 答案:(1)10.0N;(2)12.5m
答案:(1)10.0N;(2)12.5m
 (3) 当
(3) 当 时,
时, 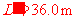 ;当
;当 时,
时, 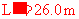
 [解析](1)设小于经过第一个圆轨道的最高点时的速度为v1根据动能定理
[解析](1)设小于经过第一个圆轨道的最高点时的速度为v1根据动能定理

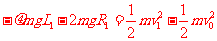 ①
①
 小球在最高点受到重力mg和轨道对它的作用力F,根据牛顿第二定律
小球在最高点受到重力mg和轨道对它的作用力F,根据牛顿第二定律

 ②
②
 由①②得
由①②得
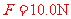 ③
③
 (2)设小球在第二个圆轨道的最高点的速度为v2,由题意
(2)设小球在第二个圆轨道的最高点的速度为v2,由题意

 ④
④

 ⑤
⑤
 由④⑤得
由④⑤得
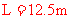 ⑥
⑥
 (3)要保证小球不脱离轨道,可分两种情况进行讨论:
(3)要保证小球不脱离轨道,可分两种情况进行讨论:
 I.轨道半径较小时,小球恰能通过第三个圆轨道,设在最高点的速度为v3,应满足
I.轨道半径较小时,小球恰能通过第三个圆轨道,设在最高点的速度为v3,应满足

 ⑦
⑦

 ⑧
⑧
 由⑥⑦⑧得
由⑥⑦⑧得
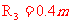
 II.轨道半径较大时,小球上升的最大高度为R3,根据动能定理
II.轨道半径较大时,小球上升的最大高度为R3,根据动能定理


 解得
解得

 为了保证圆轨道不重叠,R3最大值应满足
为了保证圆轨道不重叠,R3最大值应满足
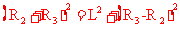
 解得
R3=27.9m
解得
R3=27.9m
 综合I、II,要使小球不脱离轨道,则第三个圆轨道的半径须满足下面的条件
综合I、II,要使小球不脱离轨道,则第三个圆轨道的半径须满足下面的条件


 或
或

 当
当 时,小球最终焦停留点与起始点A的距离为L′,则
时,小球最终焦停留点与起始点A的距离为L′,则



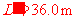
 当
当 时,小球最终焦停留点与起始点A的距离为L〞,则
时,小球最终焦停留点与起始点A的距离为L〞,则

27、(2009年天津卷)12.2008年12月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系。研究发现,有一星体S2绕人马座A*做椭圆运动,其轨道半长轴为9.50 102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上。观测得到S2星的运行周期为15.2年。
102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上。观测得到S2星的运行周期为15.2年。
(1)
 若将S2星的运行轨道视为半径r=9.50
若将S2星的运行轨道视为半径r=9.50 102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
(2)
 黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚。由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G
黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚。由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G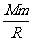 (设粒子在离黑洞无限远处的势能为零),式中M、R分别表示黑洞的质量和半径。已知引力常量G=6.7
(设粒子在离黑洞无限远处的势能为零),式中M、R分别表示黑洞的质量和半径。已知引力常量G=6.7 10-11N·m2/kg2,光速c=3.0
10-11N·m2/kg2,光速c=3.0 108m/s,太阳质量Ms=2.0
108m/s,太阳质量Ms=2.0 1030kg,太阳半径Rs=7.0
1030kg,太阳半径Rs=7.0 108m,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座A*的半径RA与太阳半径
108m,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座A*的半径RA与太阳半径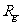 之比应小于多少(结果按四舍五入保留整数)。
之比应小于多少(结果按四舍五入保留整数)。
答案:(1)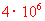 ,(2)
,(2)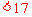
[解析](1)S2星绕人马座A*做圆周运动的向心力由人马座A*对S2星的万有引力提供,设S2星的质量为mS2,角速度为ω,周期为T,则
 ①
①
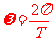 ②
②
设地球质量为mE,公转轨道半径为rE,周期为TE,则 ③
③
综合上述三式得
式中 TE=1年 ④
rE=1天文单位 ⑤
代入数据可得 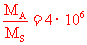 ⑥
⑥
(2)引力对粒子作用不到的地方即为无限远,此时料子的势能为零。“处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚”,说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功,粒子在到达无限远之前,其动能便减小为零,此时势能仍为负值,则其能量总和小于零,则有 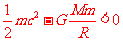 ⑦
⑦
依题意可知
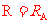 ,
,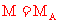
可得  ⑧
⑧
代入数据得  ⑨
⑨
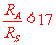 ⑩
⑩
26、 (2009年天津卷)11.如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为
(2009年天津卷)11.如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为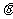 。不计空气阻力,重力加速度为g,求
。不计空气阻力,重力加速度为g,求
(1)
 电场强度E的大小和方向;
电场强度E的大小和方向;
(2)
 小球从A点抛出时初速度v0的大小;
小球从A点抛出时初速度v0的大小;
(3)
 A点到x轴的高度h.
A点到x轴的高度h.
答案:(1) ,方向竖直向上 (2)
,方向竖直向上 (2)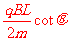 (3)
(3)
[解析](1)小球在电场、磁场中恰能做匀速圆周运动,说明电场力和重力平衡(恒力不能充当圆周运动的向心力),有
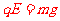 ①
①
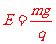 ②
②
重力的方向竖直向下,电场力方向只能向上,由于小球带正电,所以电场强度方向竖直向上。
(2)小球做匀速圆周运动,O′为圆心,MN为弦长, ,如图所示。设半径为r,由几何关系知
,如图所示。设半径为r,由几何关系知
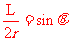 ③
③
 小球做匀速圆周运动的向心力由洛仑兹力白日提供,设小球做圆周运动的速率为v,有
小球做匀速圆周运动的向心力由洛仑兹力白日提供,设小球做圆周运动的速率为v,有
 ④
④
由速度的合成与分解知 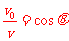 ⑤
⑤
由③④⑤式得
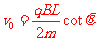 ⑥
⑥
(3)设小球到M点时的竖直分速度为vy,它与水平分速度的关系为
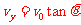 ⑦
⑦
由匀变速直线运动规律 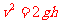 ⑧
⑧
由⑥⑦⑧式得  ⑨
⑨
25、(2009年北京卷)22.已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推到第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
答案:(1)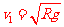 (2)
(2)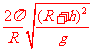
[解析](1)设卫星的质量为m,地球的质量为M,
在地球表面附近满足 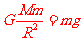
得  ①
①
卫星做圆周运动的向心力等于它受到的万有引力
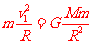 ②
②
①式代入②式,得到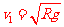
(2)考虑①式,卫星受到的万有引力为
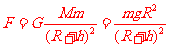 ③
③
由牛顿第二定律 ④
④
③、④联立解得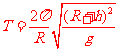
24、(2009年全国卷Ⅱ)26.如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ石油密度远小于ρ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向,当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏高,重力回速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点到附近重力加速度反常现象,已知引力常数为G
(1)设球形空腔体积为V,球心深度为d(远小于地球半径), 求空腔所引起的Q点处的重力加速度反常
求空腔所引起的Q点处的重力加速度反常
 (2)若在水平地面上半径L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积
(2)若在水平地面上半径L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积

 答案(1)
答案(1)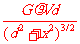
 (2)
(2)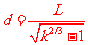 ,
,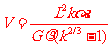
 [解析
[解析 ](1)如果将近地表的球形空腔填满密度为
](1)如果将近地表的球形空腔填满密度为 的岩石,则该地区重力加速度便回到正常值。因此,重力加速度反常可通过填充后的球形区域产生的附加引力
的岩石,则该地区重力加速度便回到正常值。因此,重力加速度反常可通过填充后的球形区域产生的附加引力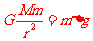 ………①来计算,式中的m是Q点处某质点的质量,M是填充后球形区域的质量,
………①来计算,式中的m是Q点处某质点的质量,M是填充后球形区域的质量, ……………②
……………②
 而r是球形空腔中心O至Q点的距离
而r是球形空腔中心O至Q点的距离 ………③
………③ 在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小。Q点处重力加速度改变的方向沿OQ方向,重力加速度反常
在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小。Q点处重力加速度改变的方向沿OQ方向,重力加速度反常 是这一改变在竖直方向上的投影
是这一改变在竖直方向上的投影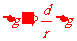 ………④联立以上式子得
………④联立以上式子得

 ,…………⑤
,…………⑤
 (2)由⑤式得,重力加速度反常
(2)由⑤式得,重力加速度反常 的最大值和最小值分别为
的最大值和最小值分别为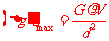 ……⑥
……⑥

 ……………⑦由提设有
……………⑦由提设有 、
、 ……⑧
……⑧
 联立以上式子得,地下球形空腔球心的深度和空腔的体积分别为
联立以上式子得,地下球形空腔球心的深度和空腔的体积分别为

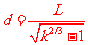 ,
,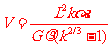
23、(2009年广东文科基础)59.关于万有引力及其应用,下列表述正确的是
A.人造地球卫星运行时不受地球引力作用
B.两物体间的万有引力跟它们质量的乘积成反比
C.两物体间的万有引力跟它们的距离成反比
D.人造卫星在地面附近绕地球作匀速圆周运动所必须具有的速度,称为第一宇宙速度
答案:D
[解析]重力是由于地球吸引而是物体受到的力,人造地球卫星运行时也受到地球的吸引,A错;根据万有引力公式F= 可知两物体间的万有引力跟它们质量的乘积成正比、跟它们之间距离的平方成反比,B、C错;近地卫星的速度等于第一宇宙速度,D对。
可知两物体间的万有引力跟它们质量的乘积成正比、跟它们之间距离的平方成反比,B、C错;近地卫星的速度等于第一宇宙速度,D对。
22、 (2009年广东文科基础)57.如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是
(2009年广东文科基础)57.如图8所示,用一轻绳系一小球悬于O点。现将小球拉至水平位置,然后释放,不计阻力。小球下落到最低点的过程中,下列表述正确的是
A.小球的机械能守恒
B.小球所受的合力不变
C.小球的动能不断减小
D.小球的重力势能增加
答案:A
[解析]小球释放后作圆周运动,受到细绳指向圆心的拉力F和竖直向下的大小不变的重力G,因为F始终指向O点,则合力始终变化,B错;F始终和速度垂直、不做功,则小球只有重力做功、机械能守恒,A对;小球的重力作正功,应用动能定理可知小球动能增加,C错;小球向下运动,位置降低(或重力作正功)、重力势能减小,D错。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com