
1.概述中国共产党领导的新民主主义革命的主要史实,认识新民主主义革命胜利的伟大意义。
2.描述匀速圆周运动的物理量
描述匀速圆周运动的物理量有线速度v、角速度ω、周期T、频率f、转速n、向心加速度a等等。
 ,它们之间的关系是:
,它们之间的关系是:

凡是直接用皮带传动(包括链条传动、摩擦传动)的两个轮子,两轮边缘上各点的线速度大小相等;凡是同一个轮轴上(各个轮都绕同一根轴同步转动)的各点角速度相等(轴上的点除外)。
 例12. 如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的线速度之比、角速度之比、加速度之比。
例12. 如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的线速度之比、角速度之比、加速度之比。
解:va= vC,而vb∶vC∶vd =1∶2∶4,所以va∶ vb∶vC∶vd =2∶1∶2∶4;ωa∶ωb=2∶1,而ωb=ωC=ωd ,所以ωa∶ωb∶ωC∶ωd =2∶1∶1∶1;再利用a=vω,可得aa∶ab∶ac∶ad=4∶1∶2∶4
 例13. 如图所示,一种向自行车车灯供电的小发电机的上端有一半径r0=1.0cm的摩擦小轮,小轮与自行车车轮的边缘接触。当车轮转动时,因摩擦而带动小轮转动,从而为发电机提供动力。自行车车轮的半径R1=35cm,小齿轮的半径R2=4.0cm,大齿轮的半径R3=10.0cm。求大齿轮的转速n1和摩擦小轮的转速n2之比。(假定摩擦小轮与自行车轮之间无相对滑动)
例13. 如图所示,一种向自行车车灯供电的小发电机的上端有一半径r0=1.0cm的摩擦小轮,小轮与自行车车轮的边缘接触。当车轮转动时,因摩擦而带动小轮转动,从而为发电机提供动力。自行车车轮的半径R1=35cm,小齿轮的半径R2=4.0cm,大齿轮的半径R3=10.0cm。求大齿轮的转速n1和摩擦小轮的转速n2之比。(假定摩擦小轮与自行车轮之间无相对滑动)
解:大小齿轮间、摩擦小轮和车轮之间和皮带传动原理相同,两轮边缘各点的线速度大小相等,由v=2πnr可知转速n和半径r成反比;小齿轮和车轮间和轮轴的原理相同,两轮上各点的转速相同。由这三次传动可以找出大齿轮和摩擦小轮间的转速之比n1∶n2=2∶175
1.匀速圆周运动的特点
匀速圆周运动是变速运动(v方向时刻在变),而且是变加速运动(a方向时刻在变)。
4.曲线运动的一般研究方法
研究曲线运动的一般方法就是正交分解。将复杂的曲线运动分解为两个互相垂直方向上的直线运动。一般以初速度或合外力的方向为坐标轴进行分解。
 例 11. 如图所示,在竖直平面的xoy坐标系内,oy表示竖直向上方向。该平面内存在沿x轴正向的匀强电场。一个带电小球从坐标原点沿oy方向竖直向上抛出,初动能为4J,不计空气阻力。它达到的最高点位置如图中M点所示。求:
例 11. 如图所示,在竖直平面的xoy坐标系内,oy表示竖直向上方向。该平面内存在沿x轴正向的匀强电场。一个带电小球从坐标原点沿oy方向竖直向上抛出,初动能为4J,不计空气阻力。它达到的最高点位置如图中M点所示。求:
⑴小球在M点时的动能E1。
⑵在图上标出小球落回x轴
时的位置N。
⑶小球到达N点时的动能E2。
解:⑴在竖直方向小球只受重力,从O→M速度由v0减小到0;在水平方向小球只受电场力,速度由0增大到v1,由图知这两个分运动平均速度大小之比为2∶3,因此v0∶v1=2∶3,所以小球在M点时的动能E1=9J。
⑵由竖直分运动知,O→M和M→N经历的时间相同,因此水平位移大小之比为1∶3,故N点的横坐标为12。
⑶小球到达N点时的竖直分速度为v0,水平分速度为2v1,由此可得此时动能E2=40J。
3. 一个有用的推论
一个有用的推论
平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
证明:设时间t内物体的水平位移为s,竖直位移为h,则末速度的水平分量vx=v0=s/t,而竖直分量vy=2h/t,  , 所以有
, 所以有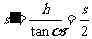
 例10. 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
例10. 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
解:以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD∶AO=2∶ ,由相似形可知vt∶v0=
,由相似形可知vt∶v0=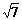 ∶
∶ ,因此很容易可以得出结论:E /=14J。
,因此很容易可以得出结论:E /=14J。
 本题也能用解析法求解。列出竖直分运动和水平分运动的方程,注意到倾角和下落高度和射程的关系,有:
或
同样可求得vt∶v0=
本题也能用解析法求解。列出竖直分运动和水平分运动的方程,注意到倾角和下落高度和射程的关系,有:
或
同样可求得vt∶v0=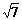 ∶
∶ ,E /=14J
,E /=14J
2.临界问题
典型例题是在排球运动中,为了使从某一位置和某一高度水平扣出的球既不触网、又不出界,扣球速度的取值范围应是多少?
 例9. 已知网高H,半场长L,扣球点高h,扣球点离网水平距离s、求:水平扣球速度v的取值范围。
例9. 已知网高H,半场长L,扣球点高h,扣球点离网水平距离s、求:水平扣球速度v的取值范围。
解:假设运动员用速度vmax扣球时,球刚好不会出界,用速度vmin扣球时,球刚好不触网,从图中数量关系可得:
 ;
;

实际扣球速度应在这两个值之间。
 当物体初速度水平且仅受重力作用时的运动,被称为平抛运动。其轨迹为抛物线,性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说,当物体所受的合外力恒定且与初速度垂直时,做类平抛运动。
当物体初速度水平且仅受重力作用时的运动,被称为平抛运动。其轨迹为抛物线,性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说,当物体所受的合外力恒定且与初速度垂直时,做类平抛运动。
1.方格问题
平抛小球的闪光照片如图。
例8. 已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
解:水平方向: 竖直方向:
竖直方向:
先求C点的水平分速度vx和竖直分速度vy,再求合速度vC:

3.连带运动问题
指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
 例6. 如图所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求v1∶v2
例6. 如图所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求v1∶v2
解:甲、乙沿绳的速度分别为v1和v2cosα,两者应该相等,所以有v1∶v2=cosα∶1
 例7. 两根光滑的杆互相垂直地固定在一起。上面分别穿有一个小球。小球a、b间用一细直棒相连如图。当细直棒与竖直杆夹角为α时,求两小球实际速度之比va∶vb
例7. 两根光滑的杆互相垂直地固定在一起。上面分别穿有一个小球。小球a、b间用一细直棒相连如图。当细直棒与竖直杆夹角为α时,求两小球实际速度之比va∶vb
解:a、b沿杆的分速度分别为vacosα和vbsinα
∴va∶vb= tanα∶1
2.过河问题
 如右图所示,若用v1表示水速,v2表示船速,则:
如右图所示,若用v1表示水速,v2表示船速,则:
①过河时间仅由v2的垂直于岸的分量v⊥决定,即 ,与v1无关,所以当v2⊥岸时,过河所用时间最短,最短时间为
,与v1无关,所以当v2⊥岸时,过河所用时间最短,最短时间为 也与v1无关。
也与v1无关。
 ②过河路程由实际运动轨迹的方向决定,当v1<v2时,最短路程为d ;当v1>v2时,最短路程程为
②过河路程由实际运动轨迹的方向决定,当v1<v2时,最短路程为d ;当v1>v2时,最短路程程为 (如右图所示)。
(如右图所示)。
1.运动的性质和轨迹
物体运动的性质由加速度决定(加速度得零时物体静止或做匀速运动;加速度恒定时物体做匀变速运动;加速度变化时物体做变加速运动)。
 物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动)。
物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动)。
两个互成角度的直线运动的合运动是直线运动还是曲线运动?
决定于它们的合速度和合加速度方向是否共线(如图所示)。
常见的类型有:
⑴a=0:匀速直线运动或静止。
⑵a恒定:性质为匀变速运动,分为:① v、a同向,匀加速直线运动;②v、a反向,匀减速直线运动;③v、a成角度,匀变速曲线运动(轨迹在v、a之间,和速度v的方向相切,方向逐渐向a的方向接近,但不可能达到。)
⑶a变化:性质为变加速运动。如简谐运动,加速度大小、方向都随时间变化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com