
3.如图所示,位于光滑固定斜面上的小物块P受到一水平向右的推力F的作用。已知物块P沿斜面加速下滑。现保持F的方向不变,使其减小,则加速度 
A.一定变小 B.一定变大 C.一定不变 
D.可能变小,可能变大,也可能不变

2.质量不计的弹簧下端固定一小球。现手持弹簧上端使小球随手在竖直方向上以同样的大小的加速度a(a<g=分别向上、向下做匀加速直线运动。若忽略空气阻力,弹簧的伸长分别为x1、x2;若空气阻力不能忽略且大小恒定,弹簧的伸长分别为 、
、 。则
。则 
 A.
A. +x1=x2+
+x1=x2+ B.
B. +x1<x2+
+x1<x2+ C.
C. +
+ =x1+x2 D.
=x1+x2 D. +
+ <x1+x2
<x1+x2
1.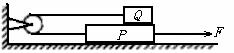 如图,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的。已知Q与P之间以及P与桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F拉P使它做匀速运动,则F的大小为
如图,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的。已知Q与P之间以及P与桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向右的力F拉P使它做匀速运动,则F的大小为

A 4μmg
B 3μmg 
C
2μmg D μmg 

3、已知 0.80.7,
0.80.7, 0.80.9,
0.80.9, 1.20.8,则
1.20.8,则 、
、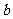 、
、 的大小关系是
的大小关系是
选做题:①比较 与
与 的大小;
的大小;
②比较 与
与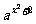 的大小
.
的大小
.
《教学设计说明》
本节课在新课标理念的指导下,本着“教师的主导地位与学生的主体地位相统一”的教学原则组织本节课的教学。采取引导发现式的教学方法并配以多媒体辅助教学,通过教师的点拨,启发学生主动思考、动手操作来达到对知识的发现和接受。本节课的教学过程设计为五个环节: 创设情境,形成概念;发现问题,探求新知 ; 深入探究,加深理解 ;强化训练,共同提高 ;小结归纳,拓展深化。在教学过程中我充分遵循学生的认知规律,在课前思考题的引领下,进入新知识的学习,而游戏情境又在学生动手操作的过程中激发学生的学习热情和探究欲望。在这些环节的铺垫中指数函数定义呼之欲出。在发现问题,探求新知和深入探究,加深理解的两个环节中均以问题为载体,通过学生合作作图、填写表格、寻求规律等一系列过程,在学生的探索与交流中解决问题,形成自己对本节课难点的理解和解决策略,从而实现重难点的突破。课堂练习由浅入深,各有侧重,不但突出了本节课的重点内容,而且让学生体会运用函数及其单调性来解题的重要思想。教学中的五个环节层层深入,环环相扣,充分体现了师生的交流互动,在教师的整体调控下,学生通过动手操作、动眼观察、动脑思考、层层递进,学生亲身经历了知识的形成和发展过程。课后思考题又将激发学生兴趣,带领学生进入对指数函数更进一步的思考和研究中,达到知识在课堂以外的延伸。
2.比较下列各题中两个值的大小 : 

(1)30.8 ,30.7;
(2)0.75-0.1,0.750.1
(3)1.012.7,1.013.5
(4)0.993.3, 0.994.5,
(5)0.60.4,0.40.6 .
1. 函数
函数 是指数函数 ,则
是指数函数 ,则
2.探究签合同问题
A先生从今天开始每天给你10万元,而你承担如下任务:第一天给A先生1元,第二天给A先生2元,,第三天给A先生4元,第四天给A先生8元,依次下去,…,A先生要和你签定15天的合同,你同意吗?又A先生要和你签定30天的合同,你能签这个合同吗?
答案:15天的合同可以签,而30 天的合同不能签.
必做题:
(1)必做题:(见后)
(2)选做题:(见后)
(3)思考题:
1.我们所学的性质是通过图象观察得到的,这些性质能不能用推理的方法得到呢 ? 如利用指数函数的值域和数值变化证明指数函数的单调性等 。
(五)小结归纳,拓展深化
(1)通过本节课的学习,你学到了那些知识?
 |
|||
|
|||
(2)你又掌握了哪些学习方法?
(3)你能将指数函数的学习与实际生活联系起来吗?
(四)当堂训练,共同提高
例 1: 比较下列各题中两个值的大小 :
(l)1.72.5,173;
(2)0.8-01,0.8-02;
(3)(0.3)-0.3,(0.2)-0.3
(4)1.70.3,0.93.1
解 :(1) 考察指数函数 y=1.7x, 由于底数 1.7〉1, 所以指数函数 y=1.7X 在 R 上是增函数
因为 2.5〈 3 , 所以 1.72.5〈1.73
(2) 考察指数函数 y = ,
由于底数0〈0.8〈 l, 所以指数函数y =
,
由于底数0〈0.8〈 l, 所以指数函数y = 在 R 上是减函数。
在 R 上是减函数。
因为 -0.1 〉-0.2,
所以 0.8-0.1〈 0.8-0.2
同底数幂比大小时 , 可构造指数函数,利用单调性比大小 .
(3) 观察图像可得,(0.3) 〈( 0.2)
〈( 0.2) 不同底数幂在比大小时 , 可利用多个指数函数图象比大小
不同底数幂在比大小时 , 可利用多个指数函数图象比大小
(4) 由指数函数的性质知
1.703 〉 1.7 0 =1,
093.1〈 0.90 =l
即 1.70.3 〉0.93.1〈 1,
所以 1.70.3 〉0.93.1
不同底数幂比大小时 , 可利用图象法或利用中间变量 ( 多选0,1)
例2:已知下列不等式
, 比较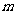 和
和 的大小 :
的大小 :
(l ) 〈
〈
(2)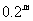 〉
〉
(3) <
< (
( 〉0)
〉0)
解:
(1) 因为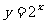 是一个单调递增函数,所以由题意
是一个单调递增函数,所以由题意
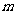 〈
〈 
(2) 因为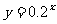 是一个单调递增函数, 所以由题意
是一个单调递增函数, 所以由题意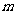 〈
〈 
(3)
当 〉1时
〉1时  是一个单调递增函数,所以此时
是一个单调递增函数,所以此时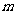 〈
〈 
当0< <1时
<1时  是一个单调递减函数, 所以此时
是一个单调递减函数, 所以此时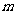 〉
〉 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com