
14.(06北京理,13)已知点
P(x,y)的坐标满足条件 点O为坐标原点,那么|PO |的最小值等于
点O为坐标原点,那么|PO |的最小值等于 ,最大值等于
,最大值等于 。
。
典型例题
EG1、已知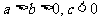 ,求证:
,求证: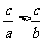 .
.
变式1:(1)如果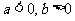 ,那么,下列不等式中正确的是( )
,那么,下列不等式中正确的是( )
A. B.
B. C.
C.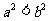 D.
D.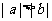
变式2:设a,b,c,d∈R,且a>b,c>d,则下列结论中正确的是( )
A.a+c>b+d B.a-c>b-d C.ac>bd D.
EG2、若关于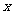 的一元二次方程
的一元二次方程 有两个不相等的实数根,求
有两个不相等的实数根,求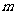 的取值范围.
的取值范围.
变式1:解关于x的不等式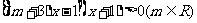

变式2:设不等式x2-2ax+a+2≤0的解集为M,如果M [1,4],求实数a的取值范围?
[1,4],求实数a的取值范围?
EG3、求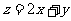 的最大值,使
的最大值,使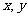 满足约束条件
满足约束条件 .
.
变式1:设动点坐标(x,y)满足 (x-y+1)(x+y-4)≥0,x≥3,则x2+y2的最小值为( )
A
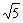 B
B
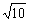 C
C
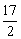 D
D 10
10
EG4、画出不等式组 表示的平面区域.
表示的平面区域.
变式1:点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是______
变式2:求不等式|x-1|+|y-1|≤2表示的平面区域的面积
EG5、
(1)把36写成两个正数的积,当这两个正数取什么值时,它们的和最小?
(2)把18写成两个正数的和,当这两个正数取什么值时,它们的积最大?
变式1:函数y =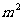 +
+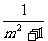 的值域为
的值域为

变式2:设x≥0, y≥0,
x2+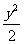 =1,则
=1,则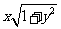 的最大值为__
的最大值为__
EG6、已知集合 ,
,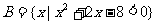 ,求
,求 .
.
变式1:已知A={x|x3+3x2+2x>0},B={x|x2+ax+b≤0}且A∩B={x|0<x≤2},A∪B={x|x>-2},求a、b的值
变式2:解关于x的不等式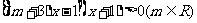

EG7、求证:
变式1:己知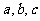 都是正数,且
都是正数,且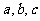 成等比数列,
成等比数列,
求证: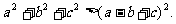
变式2:若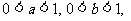 ,求证ab与
,求证ab与  不能都大于
不能都大于

EG8、要制造一个无盖的盒子,形状为长方体,底宽为2m。现有制盒材料60m2,当盒子的长、高各为多少时,盒子的体积最大?
变式1:今有一台坏天平,两臂长不等,其余均精确,有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次称量结果的和的一半就是物体的真实重量,这种说法对吗?并说明你的结论
实战训练
1(07全国2理科).不等式: >0的解集为()
>0的解集为()
(A)( -2, 1) (B) ( 2, +∞)
(C) ( -2, 1)∪ ( 2, +∞) (D) ( -∞, -2)∪ ( 1, +∞)
13.(06浙江理,3)在平面直角坐标系中,不等式组 表示的平面区域的面积是( )
表示的平面区域的面积是( )
(A)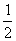 (B)
(B)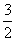 (C)
(C) (D)
(D)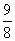
12.(06四川理,8)某厂生产甲产品每千克需用原料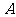 和原料
和原料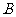 分别为
分别为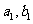 ,生产乙产品每千克需用原料
,生产乙产品每千克需用原料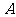 和原料
和原料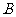 分别为
分别为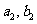 千克,甲、乙产品每千克可获利润分别为
千克,甲、乙产品每千克可获利润分别为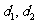 元,月初一次性够进本月用原料
元,月初一次性够进本月用原料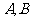 各
各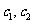 千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为
千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为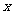 千克,
千克, 千克,月利润总额为
千克,月利润总额为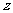 元,那么,用于求使总利润
元,那么,用于求使总利润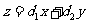 最大的数学模型中,约束条件为( )
最大的数学模型中,约束条件为( )
(A) (B)
(B)
(C) (D)
(D)
11.(06天津理,3)设变量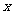 、
、 满足约束条件
满足约束条件 ,则目标函数
,则目标函数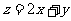 的最小值为( )
的最小值为( )
A.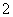 B.
B.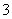 C.
C.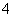 D.
D.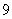
10.(1)(06安徽,10)如果实数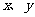 满足条件
满足条件 , 那么
, 那么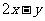 的最大值为( )
的最大值为( )
A.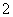 B.
B.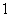 C.
C. D.
D.
9.(06山东理,3)设f(x)=
 则不等式f(x)>2的解集为( )
则不等式f(x)>2的解集为( )
(A)(1,2)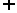 (3,+∞)
(B)(
(3,+∞)
(B)(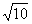 ,+∞)
,+∞)
(C)(1,2)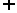 (
(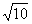 ,+∞) (D)(1,2)
,+∞) (D)(1,2)
8.在(0,2π)内,使sinx>cosx成立的x取值范围为( )
A.( ,
, )∪(π,
)∪(π,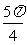 ) B.(
) B.( ,π)
,π)
C.( ,
,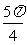 )
D.(
)
D.( ,π)∪(
,π)∪(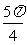 ,
,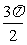 )
)
7.不等式(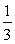 )
)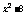 >3-2x的解集是_____。
>3-2x的解集是_____。
6.不等式组 的解集是( )
的解集是( )
A.{x|0<x<2 B.{x|0<x<2.5
B.{x|0<x<2.5 C.{x|0<x<
C.{x|0<x<
 D.{x|0<x<3
D.{x|0<x<3
5.不等式(1+x)(1-|x|)>0的解集是( )
A.{x|0≤x<1 B.{x|x<0且x≠-1
B.{x|x<0且x≠-1
C.{x|-1<x<1 D.{x|x<1且x≠-1
D.{x|x<1且x≠-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com