1.延续性动词可与表示一段时间的时间状语连用，而非延续性动词不行。

1.They________for 3 years.

　　 A.have married B.got married

　　 C.have got married D.have been married

　　 命题意图：考查动词的延续性，属于五星级题目。

　　 知识依托：延续性动词可与表示一段时间的时间状语连用。

　　 错解分析：A、C项迷惑性较大，因为学生认为其是完成时态，但marry和get married可看作非延续性动词和短语，故不能与表示一段时间的时间状语连用。

　　 解题方法与技巧：be married表状态，可以看作是延续性动词，可与表示一段时间的时间状语连用。

　　 答案：D

　　 ●锦囊妙计

2.(★★★★)Glad to see you back. How long________in Russia?

　　 A.did you stay B.have you stayed

　　 C.were you staying D.have you been staying

　　 ●案例探究

1.(★★★★★)-Susan married Jason last Sunday.

　　 -Really? How long________each other? Not more than a week,I’ m afraid.

　　 A.did they know B.have they known

　　 C.have they got to know D.had they known

(七)教师问：通过观察以上试验结果及频率图，它们的规律有什么共性呢？

(引导学生归纳)

结论：随机事件A在每次试验中是否发生是不能事先确定的，但是在进行大量重复试验后，随着试验次数的增加，事件A发生的频率总是接近于某个常数.

这个常数，我们给它起个名称，叫做概率.

4．概率的定义

一般地，在大量重复进行同一试验时，事件A发生的频率总是接近于某个常数，在它附近摆动，这时就把这个常数叫做事件A的概率，记作P(A).

这里的P是英文Probability(概率)的第一个字母.

说明：

(1)　　 概率从数量上反映了一个事件发生的可能性的大小;

(概率越大，表明事件A发生的频率越大，它发生的可能性越大；概率越小，它发生的可能性也越小)

例如：

抛一枚硬币出现“正面向上”的概率是0.5,

是指：“正面向上”可能性为50%.

任取一个乒乓球得到优等品的概率是0.95,

是指：得到优等品的可能性为95%.

(2)概率是频率的稳定值，频率是概率的近似值;

上面有关概率的定义，实际上也是求一个事件的概率的基本方法：进行大量的重复试验，用这个事件发生的频率近似地作为它的概率.

频率是否等同于概率呢？

(可以提示：频率是不是不变的？概率是不是不变的？)

频率本身是随机的，在试验前不能确定，做同样次数或不同次数的重复试验得到的事件的频率都有可能不同. 而概率是一个确定数,是客观存在的，与每次试验无关.

(3)随机事件A的概率范围.

记随机事件A在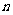次试验中发生了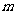次,

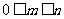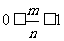那么有 , ，于是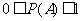

由概率的统计定义，可以得到：必然事件的概率1，不可能事件的概率是0.

从这个意义上，必然事件与不可能事件可以看作随机事件的两种极端情况.

可见，虽然它们是两类不同的事件，但在一定的情况下又可以统一起来，这也正反映了事物间既对立又统一的辨证关系．

5．课堂练习

某射手在同一条件下进行射击,结果如下表所示:

(1)　 计算表中击中靶心的各个频率;

(2)　 这个射手射击一次,击中靶心的概率约是多少?　 0.9

◆这个射手击中靶心的概率是0.9，那么他射击10次，一定能击中靶心9次吗？

答：不一定. 射击10次，相当于做了10次试验，每次试验的结果都是随机的，所以射击10次的结果也是随机的；但随着射击次数的增加，射击次数很多时，击中靶心的可能性为90%.

6．课堂小结

(1)事件的分类：必然事件、不可能事件和随机事件；

(2)随机事件概率的定义；

(3)统计的思想方法.

(让学生回顾获得概率定义的过程：试验、观察、探究、归纳和总结，进一步体会统计的思想方法 )

通过对概率知识的学习，我们知道一个随机事件的发生既有随机性(对单次试验来说)，又存在着统计规律性(对大量重复试验来说)，这里面也渗透了偶然寓于必然，事物之间既对立又统一的辨证唯物主义思想．

7．布置作业

(1)课本138页，练习 3.

(2)思考题：

随机事件的概率，一般可以通过大量的重复试验求得其近似值．那么，对于某些随机事件，比如：“抛掷一枚硬币，正面向上”，能否不通过重复试验，只从理论上的分析得出随机事件的概率呢？

(六)再让学生看另外两组试验结果，观察分析频率的变化规律.

(2)某批乒乓球质量检查结果表

抽取球数	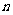50	100	200	500	1000	2000
优等品数	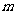45	92	194	470	954	1902
优等品频率	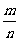0.9	0.92	0.97	0.94	0.954	0.951

可以看到，当抽查的球数很多时，抽到优等品的频率接近于常数0.95，在它附近摆动.

(3)某种油菜籽在相同条件下的发芽试验结果表

每批粒数	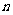2	5	10	70	130	310	700	1500	2000	3000
发芽粒数	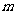2	4	9	60	116	282	639	1339	1806	2715
发芽的频率	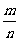1	0.8	0.9	0.857	0.892	0.910	0.913	0.893	0.903	0.905

可以看到，当试验的油菜籽的粒数很多时，油菜籽发芽的频率接近于常数0.9.

(五)教师用计算机来演示大量抛掷硬币的模拟试验，让学生进一步来体会这样一个规律.

(四)教师将组长统计的数据及历史上科学家得到的大量试验的数据输入电脑，借助Excel统计功能把频率图画出来．

(1)抛掷硬币试验结果表

抛掷次数	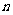2048	4040	12000	24000	30000	72088
正面向上次数	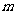1061	2048	6019	12012	14984	36124
正面向上的频率	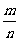0.5181	0.5069	0.5016	0.5005	0.4995	0.5011

引导学生来观察这个频率图，看一看由个人到小组、全班再到大量试验频率的变化，有什么规律？

(同学们相互讨论，请同学来回答，如果不完善，请其他同学补充，最后教师总结)

规律：“掷一枚硬币，正面向上”在一次试验中是否发生不能确定，但随着试验次数的增加，正面向上的频率逐渐地接近于0.5.

(三)试验做完后，让学生比较他们的试验结果是否相同，并请组长统计本组的结果

教师问：试验结果与其他同学比较，你的结果和他们相同吗？为什么？

因为“抛掷一枚硬币，正面向上”这个事件是一个随机事件，在每一次试验中，它的结果是随机的，所以10次的试验结果也是随机的，可能会不同.

(二)试验要求及规则

每人做 10次抛掷硬币试验，记录正面向上的次数，并计算正面向上的频率，将试验结果填入表中：

姓 名	抛掷次数(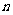)	正面向上次数(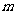)	频率()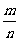
	10

抛硬币的规则：

(1)硬币统一(1角硬币)；(2)垂直下抛；(3)离桌面高度大约为一尺.

(这样的话，我们基本上在相同的条件下做试验)