
4、下列各句中,没有语病的一句是( )
A.要继续保持中国经济的平稳增长,就必须解决经济发展中不稳定、不协调、不可持续的问题。目前最大的困难是抑制物价的过快上涨和通货膨胀的压力。
B.我们更希望看到的是原生态的课堂,是真实的课堂、充满变化的课堂,而不是一切都预设好了,把学生可能有的思想、情感都装在挖好的坑里,只等着学生往里跳。
C.六方会谈在危机与转机的反复中曲折前进,其根本原因是朝美

在战略上存在巨大的差异并相互较量的结果。
D.我们一致认为,不管是贺岁电影、贺岁话剧,还是贺岁书,光靠炒作和玩概念是行不通的,毕竟赢得市场与观众的关键在于作品的质量。
3.下列句子中加点成语使用恰当的一项是( ) 
A.我国政府斥巨资力保本届奥运会万无一失,安全保卫工作可谓细致周到。战斗机在空中盘旋,舰艇在海上游弋,警察在街道巡逻:这真有点风声鹤唳的味道。
B.虽然一个阶段某些国内品牌手机也能取得巨大的市场份额,甚至可以一度与国外品牌分庭抗礼。但是由于品牌缺少“含金量”,国内品牌手机很难进入消费者心目中的“第一军团”。
C.在现场,影院特意赠送冯小刚导演一把集结号。冯导煞有介事地拿着,可还没等摸热,就被一位自称看过两遍《集结号》的热心影迷抢走了。

D.看着那些在地震中失散的灾民终于与亲人破镜重圆,相拥而泣的场面,记者都忍不住潸然泪下。
2.下列各组词语中没有错别字的一项是( ) 
A.烦燥 鞠躬尽粹 灵犀 兵慌马乱 
B.蛊惑 嗔目而视 瘐毙 脍炙人口 
C.对峙 惊惶失措 搭讪 苌弘化碧
D.盘桓 买犊还珠 矜悯 风烛残年 
1.下列加点字注音全部正确的一项是( ) 
A.窸窣(sū)
整饬(chì) 蹩脚(biē) 拾级而上(shè)
B.掮客(qián) 坍圮(qǐ) 霰弹(sǎn) 稗官野史(bài)
C.谂知(shěn) 攻讦(jié)
慰藉(jiè) 联袂表演(mèi)
D.沽酒(gū) 熨帖(yùn) 金钏(chuān) 前合后偃(yǎn)
例1.已知长方体的全面积为11,其12条棱的长度之和为24,则这个长方体的一条对角线长为( ).
(A)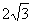 (B)
(B)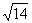 (C)5 (D)6
(C)5 (D)6
分析及解:设长方体三条棱长分别为x,y,z,则依条件得:
2(xy+yz+zx)=11,4(x+y+z)=24.而欲求的对角线长为 ,因此需将对称式
,因此需将对称式 写成基本对称式x+y+z及xy+yz+zx的组合形式,完成这种组合的常用手段是配方法.故
写成基本对称式x+y+z及xy+yz+zx的组合形式,完成这种组合的常用手段是配方法.故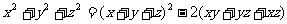 =62-11=25
=62-11=25 
∴  ,应选C.
,应选C.
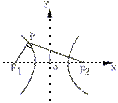 例2.设F1和F2为双曲线
例2.设F1和F2为双曲线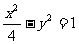 的两个焦点,点P在双曲线上且满足∠F1PF2=90°,则ΔF1PF2的面积是( ).
的两个焦点,点P在双曲线上且满足∠F1PF2=90°,则ΔF1PF2的面积是( ).
(A)1 (B) (C)2 (D)
(C)2 (D)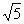

分析及解:欲求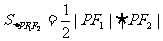 (1),而由已知能得到什么呢?
(1),而由已知能得到什么呢?
由∠F1PF2=90°,得 (2),
(2),
又根据双曲线的定义得|PF1|-|PF2|=4 (3),那么(2)、(3)两式与要求的三角形面积有何联系呢?我们发现将(3)式完全平方,即可找到三个式子之间的关系.即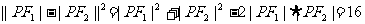 ,
,
故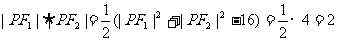

∴
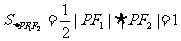 ,∴ 选(A).
,∴ 选(A).
注:配方法实现了“平方和”与“和的平方”的相互转化.
例3.设双曲线的中心是坐标原点,准线平行于x轴,离心率为 ,已知点P(0,5)到该双曲线上的点的最近距离是2,求双曲线方程.
,已知点P(0,5)到该双曲线上的点的最近距离是2,求双曲线方程.
分析及解:由题意可设双曲线方程为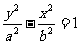 ,∵
,∵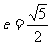 ,∴a=2b,因此所求双曲线方程可写成:
,∴a=2b,因此所求双曲线方程可写成: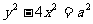 (1),故只需求出a可求解.
(1),故只需求出a可求解.
设双曲线上点Q的坐标为(x,y),则|PQ|=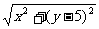 (2),∵点Q(x,y)在双曲线上,∴(x,y)满足(1)式,代入(2)得|PQ|=
(2),∵点Q(x,y)在双曲线上,∴(x,y)满足(1)式,代入(2)得|PQ|=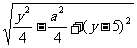 (3),此时|PQ|2表示为变量y的二次函数,利用配方法求出其最小值即可求解.
(3),此时|PQ|2表示为变量y的二次函数,利用配方法求出其最小值即可求解.
由(3)式有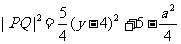 (y≥a或y≤-a).
(y≥a或y≤-a).
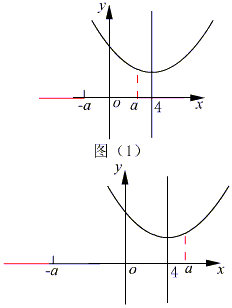 二次曲线的对称轴为y=4,而函数的定义域y≥a或y≤-a,因此,需对a≤4与a>4分类讨论.
二次曲线的对称轴为y=4,而函数的定义域y≥a或y≤-a,因此,需对a≤4与a>4分类讨论.
(1)当a≤4时,如图(1)可知函数在y=4处取得最小值,
∴令 ,得a2=4
,得a2=4
∴所求双曲线方程为 .
.
(2)当a>4时,如图(2)可知函数在y=a处取得最小值,
∴令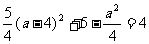 ,得a2=49,
,得a2=49,
∴所求双曲线方程为 .
.
注:此题是利用待定系数法求解双曲线方程的,其中利用配方法求解二次函数的最值问题,由于二次函数的定义域与参数a有关,因此需对字母a的取值分类讨论,从而得到两个解,同学们在解答数习题时应学会综合运用数学思想方法解题.
例4.设f(x)是一次函数,且其在定义域内是增函数,又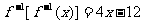 ,试求f(x)的表达式.
,试求f(x)的表达式.
分析及解:因为此函数的模式已知,故此题需用待定系数法求出函数表达式.
设一次函数y=f(x)=ax+b (a>0),可知
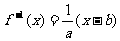 ,
,
∴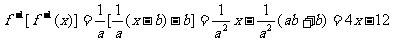 .
.
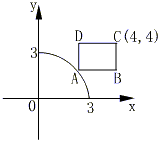 比较系数可知:
比较系数可知: 

解此方程组,得 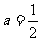 ,b=2,∴所求f(x)=
,b=2,∴所求f(x)=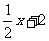 .
.
例5.如图,已知在矩形ABCD中,C(4,4),点A在曲线 (x>0,y>0)上移动,且AB,BC两边始终分别平行于x轴,y轴,求使矩形ABCD的面积为最小时点A的坐标.
(x>0,y>0)上移动,且AB,BC两边始终分别平行于x轴,y轴,求使矩形ABCD的面积为最小时点A的坐标.
分析及解:设A(x,y),如图所示,则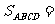 (4-x)(4-y)
(1)
(4-x)(4-y)
(1)
此时S表示为变量x,y的函数,如何将S表示为一个变量x(或y)的函数呢?有的同学想到由已知得x2+y2=9,如何利用此条件?是从等式中解出x(或y),再代入(1)式,因为表达式有开方,显然此方法不好.
如果我们将(1)式继续变形,会得到S=16-4(x+y)+xy (2)
这时我们可联想到x2+y2与x+y、xy间的关系,即(x+y)2=9+2xy.
因此,只需设t=x+y,则xy=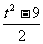 ,代入(2)式得
,代入(2)式得 
S=16-4t+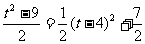 (3)S表示为变量t的二次函数,
(3)S表示为变量t的二次函数,
∵0<x<3,0<y<3,∴3<t<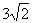 ,∴当t=4时,SABCD的最小值为
,∴当t=4时,SABCD的最小值为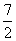 .
.
此时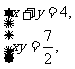
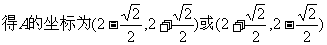

注:换元前后新旧变量的取值范围是不同的,这样才能防止出现不必要的错误.
例6.设方程x2+2kx+4=0的两实根为x1,x2,若 ≥3,求k的取值范围.
≥3,求k的取值范围.
解:∵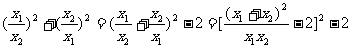 ≥3,
≥3,
以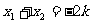 ,
,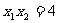 代入整理得(k2-2)2≥5,又∵Δ=4k2-16≥0,
代入整理得(k2-2)2≥5,又∵Δ=4k2-16≥0,
∴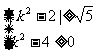 解得k∈(-
解得k∈(-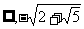 )∪[
)∪[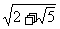 ,+
,+ ].
].
例7.点P(x,y)在椭圆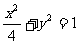 上移动时,求函数u=x2+2xy+4y2+x+2y的最大值.
上移动时,求函数u=x2+2xy+4y2+x+2y的最大值.
解:∵点P(x,y)在椭圆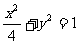 上移动, ∴可设
上移动, ∴可设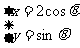 于是
于是

=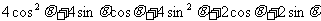
=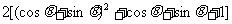
令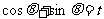 , ∵
, ∵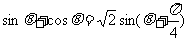 ,∴|t|≤
,∴|t|≤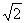 .
.
于是u=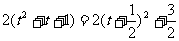 ,(|t|≤
,(|t|≤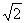 ).
).
当t=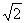 ,即
,即 时,u有最大值.
时,u有最大值.
∴θ=2kπ+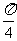 (k∈Z)时,
(k∈Z)时,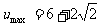 .
.
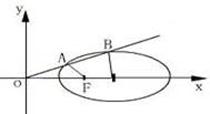 例8.过坐标原点的直线l与椭圆
例8.过坐标原点的直线l与椭圆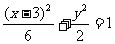 相交于A,B两点,若以AB为直径的圆恰好通过椭圆的左焦点F,求直线l的倾斜角.
相交于A,B两点,若以AB为直径的圆恰好通过椭圆的左焦点F,求直线l的倾斜角.
解:设A(x1,y1),B(x2,y2)
直线l的方程为y=kx,将它代入椭圆方
程整理得  (*)
(*)
由韦达定理,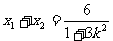 (1),
(1),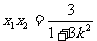 (2)
(2)
又F(1,0)且AF⊥BF,∴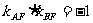 , 即
, 即 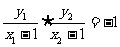 ,
,
将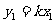 ,
,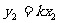 代入上式整理得
代入上式整理得  ,
,
将(1)式,(2)式代入,解得 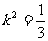 . 故直线l的倾斜角为
. 故直线l的倾斜角为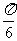 或
或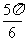 .
.
注:本题设交点坐标为参数,“设而不求”,以这些参数为桥梁建立斜率为k的方程求解.
例9.设集合A={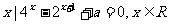 }
}
(1)若A中有且只有一个元素,求实数a的取值集合B;
(2)当a∈B时,不等式x2-5x-6<a(x-4)恒成立,求x的取值范围.
解:(1)令t=2x,则t>0且方程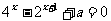 化为t2-2t+a=0
(*),A中有且只有一个元素等价于方程(*)有且只有一个正根,再令f(t)=t2-2t+a,
化为t2-2t+a=0
(*),A中有且只有一个元素等价于方程(*)有且只有一个正根,再令f(t)=t2-2t+a,
则Δ=0 或 即a=1或a≤0,从而B=(-
即a=1或a≤0,从而B=(- ,0]∪{1}.
,0]∪{1}.
(2)当a=1时,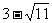 <x<3+
<x<3+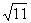 ,
,
当a≤0,令g(a)=a(x-4)-(x2-5x-6),则当a≤0时不等式 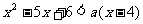 恒成立,
恒成立,
即当a≤0时,g(a)>0恒成立,故  ≤4.
≤4.
综上讨论,x的取值范围是(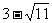 ,4).
,4).
配方法、待定系数法、换元法是几种常用的数学基本方法.这些方法是数学思想的具体体现,是解决问题的手段,它不仅有明确的内涵,而且具有可操作性,有实施的步骤和作法.
配方法是对数学式子进行一种定向的变形技巧,由于这种配成“完全平方”的恒等变形,使问题的结构发生了转化,从中可找到已知与未知之间的联系,促成问题的解决。
待定系数法的实质是方程的思想,这个方法是将待定的未知数与已知数统一在方程关系中,从而通过解方程(或方程组)求得未知数.
换元法是一种变量代换,它是用一种变数形式去取代另一种变数形式,从而使问题得到简化,换元的实质是转化.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com