
3.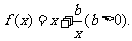
分析:为了提高解题的准确性,在利用求导的方法确定函数的单调区间时,也必须先求出函数的定义域,然后再求导判断符号,以避免不该出现的失误.
解:1.函数 的定义域为R,
的定义域为R,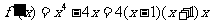
令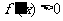 ,得
,得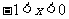 或
或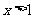 .
.
∴函数 的单调递增区间为(-1,0)和
的单调递增区间为(-1,0)和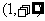 ;
;
令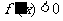 ,得
,得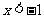 或
或 ,
,
∴函数 的单调递减区间为
的单调递减区间为 和(0,1).
和(0,1).
2.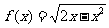 ;
;
1.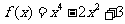 ;
;
3.函数 是奇函数,只需讨论函数在(0,1)上的单调性
是奇函数,只需讨论函数在(0,1)上的单调性
当 时,
时,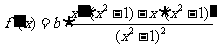

若 ,则
,则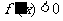 ,函数
,函数 在(0,1)上是减函数;
在(0,1)上是减函数;
若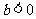 ,则
,则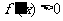 ,函数
,函数 在(0,1)上是增函数.
在(0,1)上是增函数.
又函数 是奇函数,而奇函数在对称的两个区间上有相同的单调性.所以当
是奇函数,而奇函数在对称的两个区间上有相同的单调性.所以当 时,函数
时,函数 在(-1,1)上是减函数,当
在(-1,1)上是减函数,当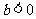 时,函数
时,函数 在(-1,1)上是增函数.
在(-1,1)上是增函数.
说明:分类讨论是重要的数学解题方法.它把数学问题划分成若干个局部问题,在每一个局部问题中,原先的“不确定因素”不再影响问题的解决,当这些局部问题都解决完时,整个问题也就解决了.在判断含参数函数的单调性时,不仅要考虑到参数的取值范围,而且要结合函数的定义域来确定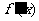 的符号,否则会产生错误判断.
的符号,否则会产生错误判断.
分类讨论必须给予足够的重视,真正发挥数学解题思想作为联系知识与能力中的作用,从而提高简化计算能力.
利用导数求函数的单调区间
例 求下列函数的单调区间:
2.函数的定义域是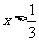 或
或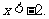
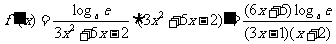
①若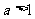 ,则当
,则当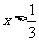 时,
时,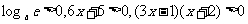 ,
,
∴ ,∴函数
,∴函数 在
在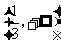 上是增函数;
上是增函数;
当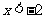 时,
时,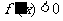 ,∴函数
,∴函数 在
在 上是减函数
上是减函数
②若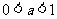 ,则当
,则当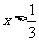 时,
时,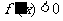 ,
,
∴函数 在
在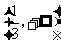 上是减函数;
上是减函数;
当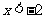 时,
时,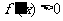 ,∴函数
,∴函数 在
在 上是增函数
上是增函数
3.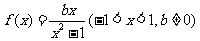 .
.
分析:利用导数可以研究函数的单调性,一般应先确定函数的定义域,再求导数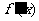 ,通过判断函数定义域被导数为零的点所划分的各区间内
,通过判断函数定义域被导数为零的点所划分的各区间内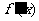 的符号,来确定函数
的符号,来确定函数 在该区间上的单调性.当给定函数含有字母参数时,分类讨论难于避免,不同的化归方法和运算程序往往使分类方法不同,应注意分类讨论的准确性.
在该区间上的单调性.当给定函数含有字母参数时,分类讨论难于避免,不同的化归方法和运算程序往往使分类方法不同,应注意分类讨论的准确性.
解: 1.函数定义域为R.
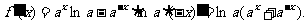
当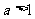 时,
时,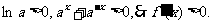
∴函数 在
在 上是增函数.
上是增函数.
当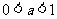 时,
时,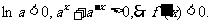
∴函数 在
在 上是减函数.
上是减函数.
2. (
(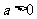 且
且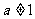 );
);
1.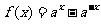 (
(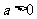 且
且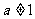 );
);
31.(8分)使用太阳能汽车是开发新能源的途径之一。有一款太阳能汽车,太阳光照射到该车电池板上的总功率为8×103W时,电池产生的电压是120V,该电压对车上电动机提供的电流是10A。问:
(1)此时电动机每分钟消耗的电能是多少焦耳?
 (2)电动机线圈的电阻为4Ω,这种情况下,太阳能汽车将太阳能转化为电动机机械能的效率多大?(机械摩擦忽略不计)
(2)电动机线圈的电阻为4Ω,这种情况下,太阳能汽车将太阳能转化为电动机机械能的效率多大?(机械摩擦忽略不计)
(3)使用太阳能有许多优点,但也有不足之处。请你写出使用太阳能的优点和不足之处各一点。
30.(6分)一个瓶子最多能装2kg的水。求:(1)该瓶子的容积;(2)用该瓶子装食用油,最多能装多少千克。(ρ水=1.0×l03kg/m3,ρ油=0.9×l03kg/m3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com