
2. ,令
,令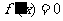 ,得
,得 ,
,
∴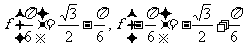 ,
,
又 .
.
∴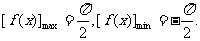
4.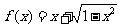 .
.
分析:函数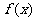 在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间
在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间 上函数的最值时,只需求出函数
上函数的最值时,只需求出函数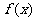 在开区间
在开区间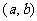 内的极值,然后与端点处函数值进行比较即可.
内的极值,然后与端点处函数值进行比较即可.
解:1.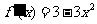 ,令
,令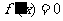 ,得
,得 ,
,
∴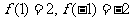 .又
.又
∴
3.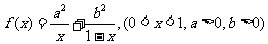
2.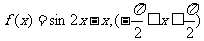 ;
;
1.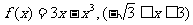 ;
;
2. .
.
若满足条件的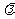 存在,则
存在,则
∵函数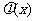 在
在 内是减函数,∴当
内是减函数,∴当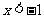 时,
时, ,
,
即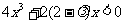 对于
对于 恒成立.
恒成立.
∴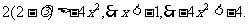
∴ ,解得
,解得 .
.
又函数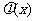 在(-1,0)上是增函数,∴当
在(-1,0)上是增函数,∴当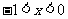 时,
时,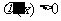
即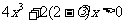 对于
对于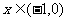 恒成立,
恒成立,
∴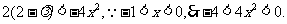
∴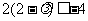 ,解得
,解得 .
.
故当 时,
时,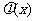 在
在 上是减函数,在(-1,0)上是增函数,即满足条件的
上是减函数,在(-1,0)上是增函数,即满足条件的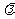 存在.
存在.
说明:函数思维实际上是辩证思维的一种特殊表现形式,它包含着运动、变化,也就存在着量与量之间的相互依赖、相互制约的关系.因此挖掘题目中的隐含条件则是打开解题思路的重要途径,具体到解题的过程,学生很大的思维障碍是迷失方向,不知从何处入手去沟通已知与未知的关系,使分散的条件相对集中,促成问题的解决.不善于应用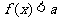 恒成立
恒成立 和
和 恒成立
恒成立 ,究其原因是对函数的思想方法理解不深.
,究其原因是对函数的思想方法理解不深.
利用导数比较大小
例 已知a、b为实数,且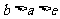 ,其中e为自然对数的底,求证:
,其中e为自然对数的底,求证: .
.
分析:通过考察函数的单调性证明不等式也是常用的一种方法.根据题目自身的特点,适当的构造函数关系,在建立函数关系时,应尽可能选择求导和判断导数都比较容易的函数,一般地,证明 ,可以等价转化为证明
,可以等价转化为证明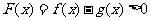 ,如果
,如果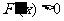 ,则函数
,则函数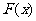 在
在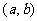 上是增函数,如果
上是增函数,如果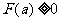 ,由增函数的定义可知,当
,由增函数的定义可知,当 时,有
时,有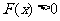 ,即
,即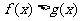 .
.
解:证法一:
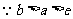 ,∴要证
,∴要证 ,只要证
,只要证 ,
,
设 ,则
,则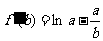 .
.
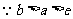 ,∴
,∴ ,且
,且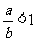 ,∴
,∴
∴函数 在
在 上是增函数.
上是增函数.
∴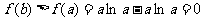 ,即
,即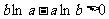 ,
,
∴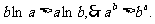
证法二:要证 ,只要证
,只要证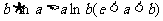 ,
,
即证 ,设
,设 ,则
,则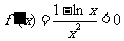 ,
,
∴函数 在
在 上是减函数.
上是减函数.
又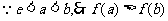 ,即
,即
说明:“构造”是一种重要而灵活的思维方式,应用好构造思想解题的关键是:一要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行逻辑组合.解决这种问题常见的思维误区是不善于构造函数或求导之后得出 的错误结论.
的错误结论.
判断函数在给定区间上的单调性
例 函数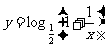 在区间
在区间 上是( )
上是( )
A.增函数,且 B.减函数,且
B.减函数,且
C.增函数,且 D.减函数,且
D.减函数,且
分析:此题要解决两个问题:一是要判断函数值y的大小;二是要判断此函数的单调性.
解:解法一:令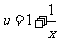 ,且
,且 ,
,
则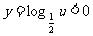 ,排除A、B.
,排除A、B.
由复合函数的性质可知,u在  上为减函数.
上为减函数.
又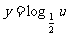 亦为减函数,故
亦为减函数,故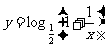 在
在  上为增函数,排除D,选C.
上为增函数,排除D,选C.
解法二:利用导数法
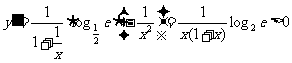
(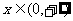 ),故y在
),故y在 上是增函数.
上是增函数.
由解法一知 .所以选C.
.所以选C.
说明:求函数的值域,是中学教学中的难关.一般可以通过图象观察或利用不等式性质求解,也可以用函数的单调性求出最大、最小值等(包括初等方法和导数法).对于复合函数的单调性问题,简单的复合函数是可以利用复合函数的性质进行判断,但是利用导数法判断一些较复杂的复合函数还是有很大优势的.
2.设 ,试问:是否存在实数
,试问:是否存在实数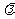 ,使
,使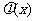 在
在 内为减函数,且在(-1,0)内是增函数.
内为减函数,且在(-1,0)内是增函数.
分析:根据题设条件可以求出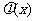 的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数
的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数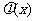 是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数
是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数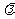 的取值范围,使问题获解.
的取值范围,使问题获解.
解:1.由题意得 ,
,
 ,
,
∴
∴
1.设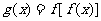 ,求
,求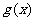 的解析式;
的解析式;
3.函数定义域为
令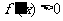 ,得
,得 或
或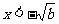 .
.
∴函数 的单调递增区间为
的单调递增区间为 和
和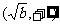 ;
;
令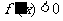 ,得
,得 且
且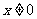 ,
,
∴函数 的单调递减区间是
的单调递减区间是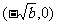 和
和 .
.
说明:依据导数在某一区间内的符号来确定函数的单调区间,体现了形象思维的直观性和运动性.解决这类问题,如果利用函数单调性定义来确定函数的单调区间,运算显得繁琐,区间难以找准.学生易犯的错误是将两个以上各自独立单调递增(或递减)区间写成并集的形式,如将例1函数 的单调递增区间和递减区间分别写成
的单调递增区间和递减区间分别写成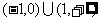 和
和 的错误结果.这里我们可以看出,除函数思想方法在本题中的重要作用之外,还要注意转化的思想方法的应用.
的错误结果.这里我们可以看出,除函数思想方法在本题中的重要作用之外,还要注意转化的思想方法的应用.
求解析式并根据单调性确定参数
例 已知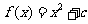 ,且
,且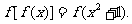
2.函数定义域为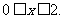

令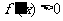 ,得
,得 .
.
∴函数 的递增区间为(0,1);
的递增区间为(0,1);
令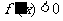 ,得
,得 ,
,
∴函数 的单调递减区间为(1,2).
的单调递减区间为(1,2).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com